题目内容
11.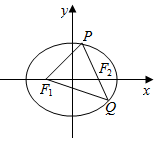 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)设F1、F2是椭圆的左、右焦点,过F2的直线与椭圆相交于P、Q两点,求△F1PQ面积的最小值.
分析 (Ⅰ)由椭圆的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,列出方程组,求出a=2,b=1,由此能求出椭圆C的方程.
(Ⅱ)设直线PQ的方程为x=ty+1,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,得(3t2+4)y2+6ty-9=0,由此利用韦达定理、弦长公式、换元法、函数单调性,结合已知条件能求出△F1PQ面积的最小值.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{2b=2\sqrt{3}}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,
∴椭圆C的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(Ⅱ)设直线PQ的方程为x=ty+1,
代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,得(3t2+4)y2+6ty-9=0,
∴${y}_{1}+{y}_{2}=-\frac{6t}{3{t}^{2}+4}$,${y}_{1}{y}_{2}=-\frac{9}{3{t}^{2}+4}$,
设P(x1,y1)<Q(x2,y2),
则${S}_{△{F}_{1}PO}$=$\frac{1}{2}•2c•|{y}_{1}-{y}_{2}|$=|y1-y2|=12•$\sqrt{\frac{{t}^{2}+1}{(3{t}^{2}+4})^{2}}$,
令u=$\sqrt{{t}^{2}+1}$∈[1,+∞),
则${S}_{△{F}_{1}PQ}=\frac{12}{3u+\frac{1}{μ}}$,
∵y=3$μ+\frac{1}{μ}$在[1,+∞)上是增函数,
∴当μ=1,即t=0时,(${S}_{△{F}_{1}PQ}$)min=3.
∴△F1PQ面积的最小值是3.
点评 本题考查椭圆方程的求法,考查三角形面积的最小值的求法,是中档题,解题时要认真审题,注意韦达定理、弦长公式、换元法、函数单调性的合理运用.

| A. | 128 | B. | 64 | C. | 96 | D. | 48 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
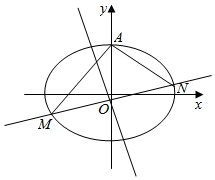 已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$
已知中心在原点O,焦点在x轴上的椭圆的一个顶点坐标为(2,0),离心率为$\frac{\sqrt{3}}{2}$