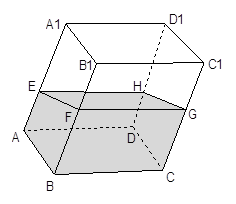
题目内容
如图在长方体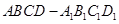 中,其中
中,其中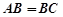 ,
,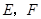 分别是
分别是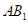 ,
, 的中点,则以下结论中
的中点,则以下结论中
① 与
与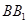 垂直; ②
垂直; ② ⊥平面
⊥平面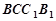 ;
;
③ 与
与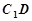 所成角为
所成角为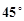 ; ④
; ④ ∥平面
∥平面
不成立的是( )
| A.②③ | B.①④ | C.③ | D.①②④ |
A
解析试题分析:因为F为BC1,所以连接B1C正好交BC1与点F,连接AC,在∆B1AC中,因为E、F分别是AB1,B1C的中点,所以EF//AC。在长方体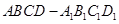 中,BB1
中,BB1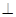 面ABCD,AC
面ABCD,AC 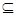 面ABCD,所以BB1
面ABCD,所以BB1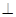 AC,又因为EF//AC,所以BB1
AC,又因为EF//AC,所以BB1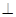 EF,因此①正确;因为AC不垂直与面
EF,因此①正确;因为AC不垂直与面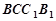 ,所以EF也不垂直面
,所以EF也不垂直面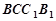 ,因此②错误;因为EF//AC,C1D//AB1,所以
,因此②错误;因为EF//AC,C1D//AB1,所以 与
与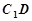 所成角为
所成角为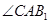 ,在长方体中,没给出高,因此
,在长方体中,没给出高,因此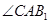 不一定是450,所以③不能立;因为AC∥平面
不一定是450,所以③不能立;因为AC∥平面 ,所以
,所以 ∥平面
∥平面 ,因此④正确。
,因此④正确。
考点:线面垂直的判定定理;线面平行的判定定理;异面直线所成的角;线线垂直的判定。
点评:做本题的关键是证出EF//AC,从而根据AC具有的一些性质,来判断EF的性质。本题涉及到的知识点较多,我们要熟练掌握每一个知识点。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
若a、b表示两条不同直线,α、β表示两个不同平面,则下列命题正确的是( )
A.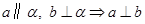 | B.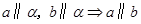 |
C.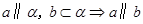 | D. |
已知两条直线 ,
, ,两个平面
,两个平面 ,
,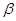 ,给出下面四个命题:
,给出下面四个命题:
①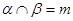 ,
,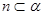
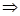
 ∥
∥ 或者
或者 ,
, 相交
相交
② ∥
∥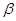 ,
, ,
,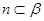
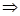
 ∥
∥
③ ∥
∥ ,
, ∥
∥
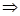
 ∥
∥
④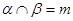 ,
,  ∥
∥
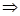
 ∥
∥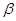 或者
或者 ∥
∥
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
正方体的一条对角线与正方体的棱可组成n对异面直线,则n等于 ( )
| A.2 | B.3 | C.6 | D.12 |
如图长方体中,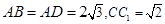 ,则二面角
,则二面角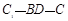 的大小为
的大小为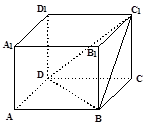
| A.300 | B.450 | C.600 | D.900 |
若 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,则下列命题中正确的是( )
是一条直线,则下列命题中正确的是( )
A.若 |
B.若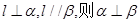 |
C.若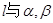 的所成角相等,则 的所成角相等,则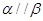 |
D.若 上有两个点到α的距离相等,则 上有两个点到α的距离相等,则 |
已知正三棱柱ABC—A1B1C1中,A1B⊥CB1,则A1B与AC1所成的角为( )
| A.450 | B.600 | C.900 | D.1200 |
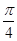 和
和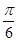 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )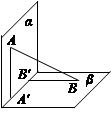
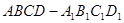 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边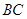 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: 的面积不改变;
的面积不改变; 始终与水面
始终与水面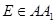 时,
时,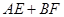 是定值.
是定值.