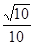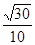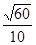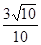题目内容
已知两条直线 ,
, ,两个平面
,两个平面 ,
,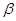 ,给出下面四个命题:
,给出下面四个命题:
①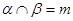 ,
,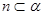
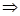
 ∥
∥ 或者
或者 ,
, 相交
相交
② ∥
∥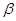 ,
, ,
,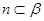
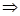
 ∥
∥
③ ∥
∥ ,
, ∥
∥
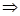
 ∥
∥
④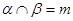 ,
,  ∥
∥
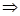
 ∥
∥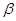 或者
或者 ∥
∥
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
C
解析试题分析:对于A,由于两个平面相交,那么在其中一个平面内的一条直线与其交线的位置关系可能只有两种,故正确。
对于B,两个平行平面中的任意一条直线之间的位置关系可能是平行也可能异面直线,因此错误。
对于C,根据线面平行的性质定理,那么直线n可能在平面 内,也可能平行。
内,也可能平行。
对于D,那么利用线面平行的判定定理,可知线线平行,则线面平行,故正确,选C.
考点:本试题考查了空间中点线面的位置关系的运用。
点评:解决该试题的关键是熟练利用线面平行的性质定理和线线平行的判定定理,考查学生分析解决问题的能力,属于中档题。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 、
、 是不同的直线,
是不同的直线, 、
、 、
、 是不同的平面,有以下四命题:
是不同的平面,有以下四命题:
① 若 ,则
,则 ; ②若
; ②若 ,则
,则 ;
;
③ 若 ,则
,则 ; ④若
; ④若 ,则
,则 .
.
其中真命题的序号是 ( )
| A.①③ | B.①④ | C.②③ | D.②④ |
若α、β是两个不同的平面,m、n是两条不同直线,则下列命题不正确的是
| A.α∥β,m⊥α,则m⊥β |
| B.m∥n,m⊥α,则n⊥α |
| C. n∥α,n⊥β,则α⊥β |
D.α β=m,n与α、β所成的角相等,则m⊥n β=m,n与α、β所成的角相等,则m⊥n |
设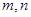 是两条不同的直线,
是两条不同的直线, 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题:
①若 ⊥
⊥ ,
,  ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则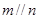 ;
;
④若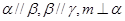 ,则
,则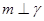 .
.
其中正确命题的序号是( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
在正方体 中,
中,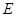 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值构成的集合是( )
所成角的正切值构成的集合是( )
A. | B. |
C. | D. |
如图在长方体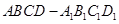 中,其中
中,其中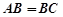 ,
,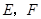 分别是
分别是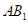 ,
, 的中点,则以下结论中
的中点,则以下结论中
① 与
与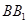 垂直; ②
垂直; ② ⊥平面
⊥平面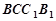 ;
;
③ 与
与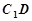 所成角为
所成角为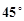 ; ④
; ④ ∥平面
∥平面
不成立的是( )
| A.②③ | B.①④ | C.③ | D.①②④ |
下列命题正确的是( )
| A.若两条直线和同一个平面所成的角相等,则这两条直线平行 |
| B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 |
| C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| D.若两个平面都垂直于第三个平面,则这两个平面平行 |
下列叙述中错误的是( )
A.若 且 且 ,则 ,则 ; ; |
B.三点 确定一个平面; 确定一个平面; |
C.若直线 ,则直线 ,则直线 与 与 能够确定一个平面; 能够确定一个平面; |
D.若 且 且 ,则 ,则 . . |