题目内容
11.已知cos($\frac{π}{4}$+α)=-$\frac{3}{5}$,且α是第三象限角,则cos($\frac{π}{4}$+2α)的值为( )| A. | $\frac{31}{50}$$\sqrt{2}$ | B. | $\frac{17}{50}$$\sqrt{2}$ | C. | -$\frac{17}{50}$$\sqrt{2}$ | D. | -$\frac{31}{50}$$\sqrt{2}$ |
分析 由已知可求范围$\frac{5π}{4}$<α+$\frac{π}{4}$<$\frac{7π}{4}$,利用同角三角函数基本关系式可求sin(α+$\frac{π}{4}$)的值,利用诱导公式,二倍角公式可求cos2α,sin2α的值,进而利用两角和的余弦函数公式即可求得cos(2α+$\frac{π}{4}$)的值.
解答 解:cos(2α+$\frac{π}{4}$)=cos2αcos$\frac{π}{4}$-sin2αsin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$(cos2α-sin2α).
∵cos(α+$\frac{π}{4}$)=-$\frac{3}{5}$,π<α<$\frac{3π}{2}$,可得:$\frac{5π}{4}$<α+$\frac{π}{4}$<$\frac{7π}{4}$,
∴sin(α+$\frac{π}{4}$)=-$\sqrt{1-co{s}^{2}(α+\frac{π}{4})}$=-$\frac{4}{5}$,
∴从而cos2α=sin(2α+$\frac{π}{2}$)=2sin(α+$\frac{π}{4}$)cos(α+$\frac{π}{4}$)=$\frac{24}{25}$,
sin2α=-cos(2α+$\frac{π}{2}$)=1-2cos2(α+$\frac{π}{4}$)=$\frac{7}{25}$,
∴cos(2α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$×($\frac{24}{25}$-$\frac{7}{25}$)=$\frac{17\sqrt{2}}{50}$.
故选:B.
点评 本题主要考查了同角三角函数基本关系式,诱导公式,二倍角公式,两角和的余弦函数公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | (-∞,0] | B. | (-∞,ln2-$\frac{1}{2}$] | C. | (-∞,0) | D. | (-∞,ln2-$\frac{1}{2}$) |
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |

| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )
已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )| A. | (0,1),(4,+∞) | B. | (-∞,1) | C. | (1,+∞) | D. | (-∞,0),(1,4) |
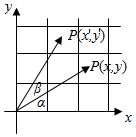 如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.