题目内容
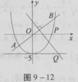
设直线l与椭圆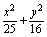 =1相交于A、B两点,l又与双曲线x2-y2=1相交于C、D两点,C、D三等分线段AB,求直线l的方程
=1相交于A、B两点,l又与双曲线x2-y2=1相交于C、D两点,C、D三等分线段AB,求直线l的方程
解法一:首先讨论l不与x轴垂直时的,情况.
设直线l的方程为y=kx+b,如图所示,l与椭圆、双曲线的交点为:A(x1,y1)、B(x2, y2)、C(x3,y3)、D(x4,y4),依题意有 .
.
由 得(16+25k2)x2+50bkx+(25b2-400)=0.(1)
得(16+25k2)x2+50bkx+(25b2-400)=0.(1)
所以x1+x2=-
由 得(1-k2+x2-2bkx-(b2+1)=0.
得(1-k2+x2-2bkx-(b2+1)=0.






练习册系列答案
相关题目
 中
中 ,则
,则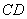 与平面
与平面 所成角的正弦值等于
所成角的正弦值等于  B.
B. C.
C. D.
D.
 (a-c)<0
(a-c)<0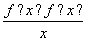 <0的解集为( ).
<0的解集为( ). A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)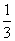 ax3-
ax3-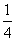 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.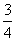 x2-bx+
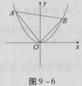
x2-bx+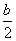 -
-
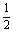 x严与抛物线y=
x严与抛物线y=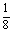 x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.