题目内容
11.设一球的半径为$tan\frac{7π}{6}$,则该球的表面积、体积分别为$\frac{4}{3}π$、$\frac{4\sqrt{3}}{27}π$.分析 直接求出半径,利用球的表面积公式以及体积公式求解即可.
解答 解:一球的半径为$tan\frac{7π}{6}$=$\frac{\sqrt{3}}{3}$,
则该球的表面积为:4π${(\frac{\sqrt{3}}{3})}^{2}$=$\frac{4}{3}π$;
体积为:$\frac{4}{3}π•{(\frac{\sqrt{3}}{3})}^{3}$=$\frac{4\sqrt{3}}{27}π$.
故答案为:$\frac{4}{3}π$;$\frac{{4\sqrt{3}}}{27}π$.
点评 本题考查球的表面积与体积的求法,考查计算能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6.直线y=kx+2与圆x2+(y-1)2=4的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 与k的取值有关 |
16.平面α⊥平面β的一个充分条件是( )
| A. | 存在一条直线l、l⊥α、l⊥β | B. | 存在一个面r、r∥α、r∥β | ||
| C. | 存在一个平面r、r⊥α、r⊥β | D. | 存在一条直线l、l⊥α、l∥β |
20.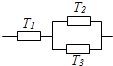 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{15}{32}$ | D. | $\frac{17}{32}$ |
 如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.
如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.