题目内容
已知函数f(x)=
,g(x)=f(x)-x,则函数g(x)的零点是0,1和 .
|
考点:函数的零点
专题:函数的性质及应用
分析:当0<x≤2时,-2<x-2≤0,可得f(x)=(x-2)2∈[0,4).同理x∈(2,4],f(x)=(x-4)2
∈(0,4],x>4,f(x)<4.如图所示,当x≤0时,由x2=x;当0<x≤2时,由(x-2)2=x,;当2<x≤4时,由(x-4)2=x.当x>4,f(x)<4,与y=x无交点.即可得出.
∈(0,4],x>4,f(x)<4.如图所示,当x≤0时,由x2=x;当0<x≤2时,由(x-2)2=x,;当2<x≤4时,由(x-4)2=x.当x>4,f(x)<4,与y=x无交点.即可得出.
解答:
解:当0<x≤2时,-2<x-2≤0,∴f(x)=(x-2)2∈[0,4),同理x∈(2,4],f(x)=(x-4)2∈(0,4],x>4,f(x)<4.
如图所示,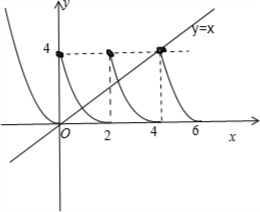
当x≤0时,由x2=x,解得x=0;
当0<x≤2时,由(x-2)2=x,解得x=1;
当2<x≤4时,由(x-4)2=x,解得x=
.
当x>4,f(x)<4,与y=x无交点.
综上可得:函数g(x)的零点是0,1和
.
故答案为:
.
如图所示,

当x≤0时,由x2=x,解得x=0;
当0<x≤2时,由(x-2)2=x,解得x=1;
当2<x≤4时,由(x-4)2=x,解得x=
9-
| ||
| 2 |
当x>4,f(x)<4,与y=x无交点.
综上可得:函数g(x)的零点是0,1和
9-
| ||
| 2 |
故答案为:
9-
| ||
| 2 |
点评:本题考查了分段函数的图象与性质、分类讨论的思想方法,考查了推理能力与数形结合的思想方法,属于难题.

练习册系列答案
相关题目