题目内容
10. 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.(Ⅰ)过BC的截面交AA1于P点,若△PBC为等边三角形,求出点P的位置;
(Ⅱ)在(Ⅰ)条件下,求四棱锥P-BCC1B1与三棱柱ABC-A1B1C1的体积比.
分析 (Ⅰ)利用勾股定理求解三角形的边长,推出P的位置.
(Ⅱ)求出四棱锥P-BCC1B1与三棱柱ABC-A1B1C1的体积,即可得到比值.
解答 解:(Ⅰ)由题意$PC=PB=2\sqrt{2}$,(2分)
在三棱柱中,由AA1⊥平面ABC,且AB=AC=2
可得:PA=2,(4分)
故点P的位置为AA1的三等分点,且靠近A1处. (6分)
(Ⅱ)由(Ⅰ)可知,${V_{ABC-{A_1}{B_1}{C_1}}}=\frac{1}{2}×2×2×3=6$,(7分)
${V_{P-{A_1}{B_1}{C_1}}}=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$(8分)
${V_{P-ABC}}=\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$,(9分)
所以${V_{P-BC{C_1}{B_1}}}=6-\frac{4}{3}-\frac{2}{3}=4$,
所以所求两个几何体的体积比为$\frac{2}{3}$. (12分)
故答案为:(Ⅰ)点P的位置为AA1的三等分点,且靠近A1处;(Ⅱ)体积比为$\frac{2}{3}$.
点评 本题考查几何体的体积的计算,直线与平面垂直的性质的应用,判断计算能力.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
20.若某几何体的三视图如图所示,则此几何体的表面积为( )
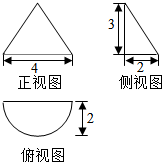

| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
15.已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-4x+1,x>0}\\{-1+{{log}_2}(-x),x<0}\end{array}}$,若函数g(x)=f(x)-a有三个不同的零点x1,x2,x3,则x1+x2+x3的取值范围是( )
| A. | (0,4) | B. | (-4,0) | C. | $(0,\frac{15}{4})$ | D. | $(\frac{1}{2},2)$ |
 如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.