题目内容
20.若a,b在区间(0,1)内,则椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1在第一象限内有两个不同的交点的概率为1-$\frac{π}{4}$.分析 椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1联立,利用椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1在第一象限内有两个不同的交点,确定a,b的关系,求出相应的面积,即可求出概率.
解答 解:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与直线l:x+y=1联立,可得(b2+a2)x2-2a2x+a2-a2b2=0,
△=4a4-4(b2+a2)(a2-a2b2)>0,
∴b2+a2>1,
∵a,b在区间(0,1)内,
∴满足条件的区域的面积为1-$\frac{π}{4}$,
又a,b在区间(0,1)内,面积为1,
∴所求的概率为1-$\frac{π}{4}$.
故答案为:1-$\frac{π}{4}$.
点评 本题考查几何概型概率的计算,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知数列{an}的首项a1=1,前n项和为Sn,且Sn+1=2Sn+n+1(n∈N*)
(1)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)求数列{nan+n}的前n项和Tn.
(1)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)求数列{nan+n}的前n项和Tn.
11.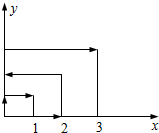 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
 如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
如图:一个质点在第一象限运动,在第一秒钟它由原点运动到点(0,1),而后接着按图所示在与x轴y轴平行的方向运动,且每秒移动一个单位长度,那么416秒后,这个质点所处的位置的坐标是(20,16).
10.命题“若x2<9,则-3<x<3”的逆否命题是( )
| A. | 若x2≥9,则x≥3或x≤-3 | B. | 若-3<x<3,则x2<9 | ||
| C. | 若x>3或x<-3,则x2>9 | D. | 若x≥3或x≤-3,则x2≥9 |