题目内容
若将一个圆锥的侧面沿着一条母线剪开,其展开图是半径为2的半圆,则该圆锥的体积为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:半径为2的半圆的弧长是2π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是2π,利用弧长公式计算底面半径后利用勾股定理求圆锥的高即可求解圆锥的体积.
解答:
解:一个圆锥的母线长为2,它的侧面展开图为半圆,
圆的弧长为:2π,即圆锥的底面周长为:2π,
设圆锥的底面半径是r,则得到2πr=2π,
解得:r=1,
这个圆锥的底面半径是1,
∴圆锥的高为
=
.
∴圆锥的体积为:
πr2h=
.
故答案为:
.
圆的弧长为:2π,即圆锥的底面周长为:2π,
设圆锥的底面半径是r,则得到2πr=2π,
解得:r=1,
这个圆锥的底面半径是1,
∴圆锥的高为
| 4-1 |
| 3 |
∴圆锥的体积为:
| 1 |
| 3 |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
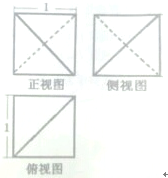
某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
某房地产公司计划出租70套相同的公寓房.当每套房月租金定为3000元时,这70套公寓能全租出去;当月租金每增加50元时(设月租金均为50元的整数倍),就会多一套房子不能出租.设租出的每套房子每月需要公司花费100元的日常维修等费用(设租不出的房子不需要花这些费用).要使公司获得最大利润,每套房月租金应定为( )
| A、3000元 |
| B、3100元 |
| C、3300元 |
| D、3500元 |
设双曲线
+
=1的离心率为2,且一个焦点与抛物线x2=8y的焦点相同,则此双曲线的方程为( )
| x2 |
| m |
| y2 |
| n |
A、
| ||||
B、
| ||||
C、y2-
| ||||
D、
|