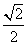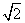题目内容
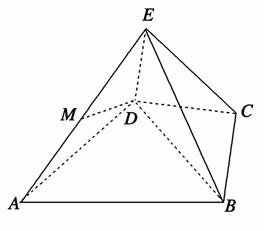
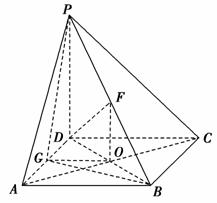
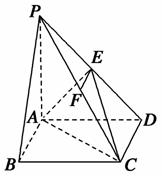
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,F是PB的中点.
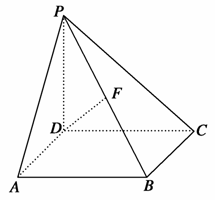
(1)求证:DF⊥AP.
(2)在线段AD上是否存在点G,使GF⊥平面PBC?若存在,说明G点的位置,并证明你的结论;若不存在,说明理由.
[证明] (1)取AB的中点E,则PA∥EF.设PD=DC=a,易求得DE=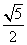 a,FE=
a,FE=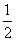 PA=
PA=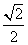 a,DF=
a,DF=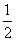 PB=
PB=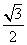 a.
a.
由于DE2=EF2+DF2,故DF⊥EF,
又EF∥PA,∴DF⊥PA.
(2)在线段AD上存在点G,使GF⊥平面PBC,且G点是AD的中点.
取AD的中点G,连接PG、BG,则PG=BG.又F为AB的中点,故GF⊥PB.
∵F为PB中点,
∴F点在底面ABCD上的射影为正方形ABCD的中心O,
∴FO⊥平面ABCD,∵BC⊂平面ABCD,∴FO⊥BC.
∵G为AD中点,O为正方形ABCD中心,∴GO⊥BC,
又GO∩FO=0,∴BC⊥平面GOF,∴GF⊥BC.
∵BC、PB是平面PBC内的两条相交直线,
∴GF⊥平面PBC.

练习册系列答案
相关题目
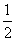 B.
B.