题目内容
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=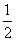 BC.
BC.
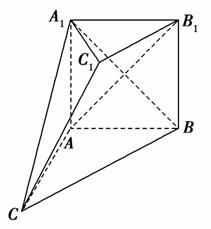
(1)求证:平面A1AC⊥平面ABC;
(2)求证:AB1∥平面A1C1C.
[证明] (1)∵四边形ABB1A1为正方形,
∴A1A=AB=AC=1,A1A⊥AB.

∴A1B=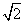 .
.
∵A1C=A1B,∴A1C=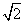 ,
,
∴∠A1AC=90°,∴A1A⊥AC.
∵AB∩AC=A,∴A1A⊥平面ABC.
又∵A1A⊂平面A1AC,
∴平面A1AC⊥平面ABC.
(2)取BC的中点E,连接AE,C1E,B1E.
∵B1C1∥BC,B1C1=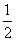 BC,
BC,
∴B1C1∥EC,B1C1=EC,
∴四边形CEB1C1为平行四边形.∴B1E∥C1C.
∵C1C⊂平面A1C1C,B1E⊄平面A1C1C,
∴B1E∥平面A1C1C.
∵B1C1∥BC,B1C1=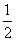 BC,
BC,
∴B1C1∥BE,B1C1=BE,
∴四边形BB1C1E为平行四边形,
∴B1B∥C1E,且B1B=C1E.
又∵四边形ABB1A1是正方形,
∴A1A∥C1E,且A1A=C1E,
∴四边形AEC1A1为平行四边形,∴AE∥A1C1.
∵A1C1⊂平面A1C1C,AE⊄平面A1C1C,
∴AE∥平面A1C1C.
∵AE∩B1E=E,∴平面B1AE∥平面A1C1C.
∵AB1⊂平面B1AE,∴AB1∥平面A1C1C.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
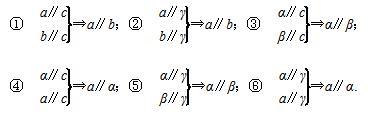 其中正确的命题是________(将正确命题的序号都填上).
其中正确的命题是________(将正确命题的序号都填上).