题目内容
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为长方形,AD=2AB,点E、F分别是线段PD、PC的中点.
(1)证明:EF∥平面PAB;
(2)在线段AD上是否存在一点O,使得BO⊥平面PAC,若存在,请指出点O的位置,并证明BO⊥平面PAC;若不存在,请说明理由.
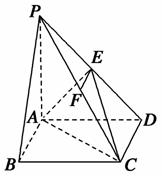
[解析] (1)证明:∵EF∥CD,CD∥AB,∴EF∥AB,
又∵EF⊄平面PAB,AB⊂平面PAB,
∴EF∥平面PAB.

(2)在线段AD上存在一点O,使得BO⊥平面PAC,此时点O为线段AD的四等分点,且AO= AD,
AD,
∵PA⊥底面ABCD,∴PA⊥BO,
又∵长方形ABCD中,AD=2AB,
∴△ABO △DAC,∴∠ABO+∠BAC=∠DAC+∠BAC=90°,∴AC⊥BO,
△DAC,∴∠ABO+∠BAC=∠DAC+∠BAC=90°,∴AC⊥BO,
又∵PA∩AC=A,
∴BO⊥平面PAC.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
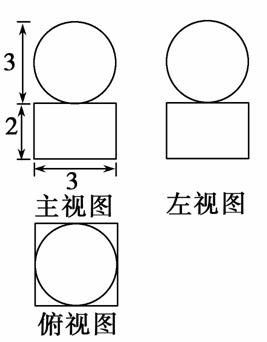
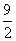 π+12 B.
π+12 B.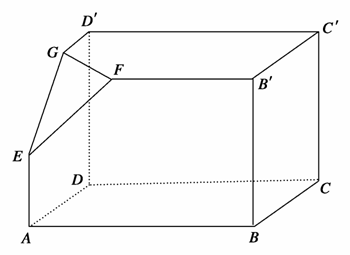
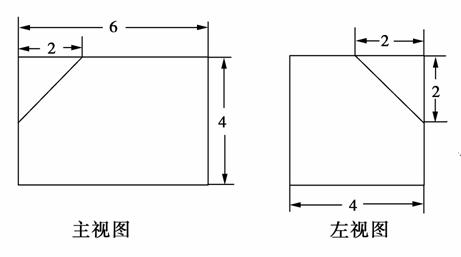
 B.
B. C.
C.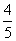 D.
D.