题目内容
12．函数y=（x-x3）•2|x|在区间[-3，3]上的图象大致是（ ）| A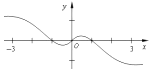． |  | B． |  | ||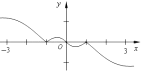
| C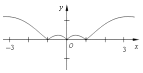． |  | D． |  |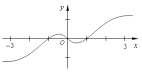
分析 利用函数的奇偶性，排除选项，然后利用特殊值判断函数的图形即可．
解答 解：函数y=（x-x3）•2|x|在区间[-3，3]上是奇函数，排除：C，
又x=$\frac{1}{2}$时，y=（$\frac{1}{2}-$$\frac{1}{8}$）×${2}^{\frac{1}{2}}$=$\frac{3\sqrt{2}}{8}$＞0．即（$\frac{1}{2}$，$\frac{3\sqrt{2}}{8}$）在函数的图象上，排除B，D，
故选：A．
点评 本题考查函数的图象的判断，注意函数的奇偶性以及特殊点的位置的判断与应用．
练习册系列答案
相关题目
在如图所示的几何体中，AF⊥平面ABCD，EF∥AB，四边形ABCD为矩形，AD=2，AB=AF=2EF=1，P是棱DF的中点．
7．已知变量x，y线性负相关，且由观测数据算得样本平均数$\overline x=3$，$\overline y=3.5$，则由该观测数据算得的线性回归方程可能是（ ）
| A． | y=0.4x+2.4 | B． | y=2x+2.4 | C． | y=-2x+9.5 | D． | y=-0.3x+4.4 |
17．传统文化就是文明演化而汇集成的一种反映民族特质和风貌的民族文化，是民族历史上各种思想文化、观念形态的总体表征．教育部考试中心确定了2017年普通高考部分学科更注重传统文化考核．某校为了了解高二年级中国数学传统文化选修课的教学效果，进行了一次阶段检测，并从中随机抽取80名同学的成绩，然后就其成绩分为A、B、C、D、E五个等级进行数据统计如下：
根据以上抽样调查数据，视频率为概率．
（1）若该校高二年级共有1000名学生，试估算该校高二年级学生获得成绩为B的人数；
（2）若等级A、B、C、D、E分别对应100分、80分、60分、40分、20分，学校要求“平均分达60分以上”为“教学达标”，请问该校高二年级此阶段教学是否达标？
（3）为更深入了解教学情况，将成绩等级为A、B的学生中，按分层抽样抽取7人，再从中任意抽取2名，求恰好抽到1名成绩为A的概率．
| 成绩 | 人数 |
| A | 9 |
| B | 12 |
| C | 31 |
| D | 22 |
| E | 6 |
（1）若该校高二年级共有1000名学生，试估算该校高二年级学生获得成绩为B的人数；
（2）若等级A、B、C、D、E分别对应100分、80分、60分、40分、20分，学校要求“平均分达60分以上”为“教学达标”，请问该校高二年级此阶段教学是否达标？
（3）为更深入了解教学情况，将成绩等级为A、B的学生中，按分层抽样抽取7人，再从中任意抽取2名，求恰好抽到1名成绩为A的概率．
4．若双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线与圆x2+y2-4y+3=0相切，则该双曲线C的离心率为（ ）
| A． | $2\sqrt{3}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |