题目内容
1.已知数列{an}的前n项和为Sn,且满足4Sn=an+1(n∈N*),设bn=log3|an|,则数列{bn}的通项公式为bn=-n..分析 利用递推关系与等比数列的通项公式可得an.
解答 解:∵4Sn=an+1(n∈N*),∴4a1=a1+1,解得a1=$\frac{1}{3}$.
n≥2时,4an=4(Sn-Sn-1)=an-an-1,可得${a}_{n}=-\frac{1}{3}{a}_{n-1}$,
∴数列{an}是等比数列,公比为-$\frac{1}{3}$.
∴an=$\frac{1}{3}×(-\frac{1}{3})^{n-1}$.
∴bn=log3|an|=$lo{g}_{3}{3}^{-n}$=-n,
故答案为:bn=-n.
点评 本题考查了数列递推关系、等比数列的通项公式、对数函数的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0\;\;,\;\;b>0})$的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | C. | $\frac{x^2}{80}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{20}-\frac{y^2}{80}=1$ |
16.已知x,y∈(0,+∞),且满足$\frac{1}{x}+\frac{1}{2y}=1$,那么x+4y的最小值为( )
| A. | $3-\sqrt{2}$ | B. | $3+2\sqrt{2}$ | C. | $3+\sqrt{2}$ | D. | $4\sqrt{2}$ |
6.“a2>b2”是“lna>lnb”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.2016年是红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神,首先在甲、乙、丙、丁四个不同的公园进行支持签名活动.
然后再各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(3)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):
据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
临界值表:
参考公式:K2=$\frac{k(ad-bc)}{(a+b)(c+d)(a+c)(b+d)}$.
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
(1)求此活动中各公园幸运之星的人数;
(2)若乙公园中每位幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(3)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):
| 有兴趣 | 无兴趣 | 合计 | |
| 男 | 25 | 5 | 30 |
| 女 | 15 | 15 | 30 |
| 合计 | 40 | 20 | 60 |
临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
11.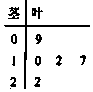 如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )
如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )
 如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )
如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )| A. | 14,12 | B. | 12,14 | C. | 14,10 | D. | 10,12 |