题目内容
已知数列{an}的前n项和为sn,a1=1,当n∈N+有an+1=
+n+1.
(1)求{an}的通项公式
(2)记bn=
,求证:b1+b2+…+bn≤
.
| Sn |
| n |
(1)求{an}的通项公式
(2)记bn=
| 1 | ||
|
| 2n-1 |
考点:数列递推式,数列的求和
专题:计算题,等差数列与等比数列
分析:(1)由an+1=
+n+1,得nan+1=Sn+n2+n①,(n-1)an=Sn-1+(n-1)2+(n-1)②(n≥2),两式相减可得递推式,由递推式可判断数列为等差数列,注意检验n=1时情形;
(2)易求bn,用数学归纳法可证明;
| Sn |
| n |
(2)易求bn,用数学归纳法可证明;
解答:
解:(1)由an+1=
+n+1,得nan+1=Sn+n2+n①,
(n-1)an=Sn-1+(n-1)2+(n-1)②(n≥2),
①-②得nan+1-(n-1)an=an+2n,即an+1-an=2(n≥2),
又a2=S1+2,∴a2-a1=2,
∴{an}为等差数列,首项为1,公差为2,
∴an=1+(n-1)•2=2n-1.
(2)由(1)知,bn=
=
,
则b1+b2+…+bn≤
即为1+
+…+
≤
,
①当n=1时,左边=1,右边=1,不等式成立;
②假设n=k时,不等式成立,即1+
+…+
≤
,
则n=k+1时,1+
+…+
+
≤
+
=
<
=
,
∴n=k+1时不等式也成立;
综上,b1+b2+…+bn≤
.
| Sn |
| n |
(n-1)an=Sn-1+(n-1)2+(n-1)②(n≥2),
①-②得nan+1-(n-1)an=an+2n,即an+1-an=2(n≥2),
又a2=S1+2,∴a2-a1=2,
∴{an}为等差数列,首项为1,公差为2,
∴an=1+(n-1)•2=2n-1.
(2)由(1)知,bn=
| 1 | ||
|
| 1 | ||
|
则b1+b2+…+bn≤
| 2n-1 |
| 1 | ||
|
| 1 | ||
|
| 2n-1 |
①当n=1时,左边=1,右边=1,不等式成立;
②假设n=k时,不等式成立,即1+
| 1 | ||
|
| 1 | ||
|
| 2k-1 |
则n=k+1时,1+
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2k-1 |
| 1 | ||
|
| ||
|
| 2k+1 | ||
|
| 2k+1 |
∴n=k+1时不等式也成立;
综上,b1+b2+…+bn≤
| 2n-1 |
点评:该题考查由数列递推式求数列通项、不等式的证明等知识,考查学生的运算求解能力.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
若曲线f(x)=asinx+1在x=0处的切线斜率为2,则(ax2-
)5展开式中x的系数为( )
| 1 |
| x |
| A、40 | B、10 |
| C、-10 | D、-40 |
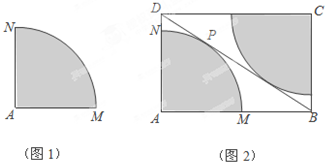 某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).
某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).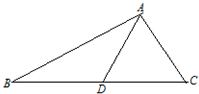 如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且
如图,在△ABC中,D是BC上的点,∠C=∠D=2∠DAB,△BAD的面积与△CAD的面积相等,且