题目内容
1．若f（x）=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}（2x-1）}}$，则f（x+1）的定义域为（ ）| A． | （-$\frac{1}{2}$，0） | B． | （-$\frac{1}{2}$，0] | C． | （-$\frac{1}{2}$，+∞） | D． | （0，+∞） |
分析 根据对数函数的性质求出函数的定义域即可．
解答 解：由题意得：0＜2x-1＜1，解得：$\frac{1}{2}$＜x＜1，
故f（x）的定义域是（$\frac{1}{2}$，1），
由$\frac{1}{2}$＜x+1＜1，解得：-$\frac{1}{2}$＜x＜0，
故函数f（x+1）的定义域是（-$\frac{1}{2}$，0），
故选：A．
点评 本题考查了求函数的定义域问题，考查对数函数的性质，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
9．已知a，b∈R，且ex≥a（x-1）+b对x∈R恒成立，则ab的最大值是（ ）
| A． | $\frac{1}{2}{e^3}$ | B． | $\frac{{\sqrt{2}}}{2}{e^3}$ | C． | $\frac{{\sqrt{3}}}{2}{e^3}$ | D． | e3 |
6．已知函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤|f（$\frac{π}{6}$）|对x∈R恒成立，且f（$\frac{π}{2}$）＞f（π），则f（x）的单调递增区间是（ ）
| A． | [kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$]（k∈Z） | B． | [kπ，kπ+$\frac{π}{2}$]（k∈Z） | C． | [kπ-$\frac{π}{6}$，kπ+$\frac{2π}{3}$]（k∈Z） | D． | [kπ-$\frac{π}{2}$，kπ]（k∈Z） |
13．方程x2+y2+Dx+Ey+F=0表示以（-2，3）为圆心，4为半径的圆，则D，E，F的值分别为（ ）
| A． | 4，-6，3 | B． | -4，6，3 | C． | -4，-6，3 | D． | 4，-6，-3 |
10．
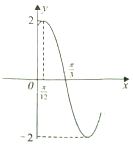函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，把f（x）的图象向右平移$\frac{π}{3}$个单位长度得到g（x）的图象，则g（x）的单调递增区间是（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，把f（x）的图象向右平移$\frac{π}{3}$个单位长度得到g（x）的图象，则g（x）的单调递增区间是（ ）| A． | $[{kπ-\frac{5π}{12}，kπ+\frac{π}{12}}]，k∈z$ | B． | $[{kπ-\frac{π}{6}，kπ+\frac{π}{3}}]，k∈z$ | ||
| C． | $[{kπ-\frac{π}{12}，kπ+\frac{5π}{12}}]，k∈z$ | D． | $[{kπ+\frac{π}{6}，kπ+\frac{5π}{6}}]，k∈z$ |