题目内容
10.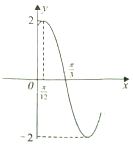 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )| A. | $[{kπ-\frac{5π}{12},kπ+\frac{π}{12}}],k∈z$ | B. | $[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈z$ | ||
| C. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}],k∈z$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{5π}{6}}],k∈z$ |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式;再根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用正弦函数的单调性求得得g(x)的单调递增区间.
解答 解:函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
可得A=2,$\frac{T}{4}$=$\frac{1}{4}•\frac{2π}{ω}$=$\frac{π}{3}$-$\frac{π}{12}$,∴ω=2.
再根据五点法作图可得2•$\frac{π}{3}$+φ=π,∴φ=$\frac{π}{3}$,∴f(x)=2sin(2x+$\frac{π}{3}$).
把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)=2sin(2x-$\frac{π}{3}$)的图象,
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,求得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
可得g(x)的单调递增区间是[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.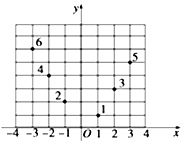 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )| A. | 1002 | B. | 1004 | C. | 1007 | D. | 1009 |
1.若f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x-1)}}$,则f(x+1)的定义域为( )
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0] | C. | (-$\frac{1}{2}$,+∞) | D. | (0,+∞) |
18.下列说法正确的是( )
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
18.已知函数f(x)=$\frac{1}{2}$ax2+bx+1,其中a∈{2,4},b∈{1,3},从f(x)中随机抽取1个,则它在(-∞,-1]上是减函数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |