题目内容
11.在棱长均为6的三棱锥纸盒内放一个小正方体,正方体可以绕某对称轴(即相对两面的中心连线)旋转,则该正方体棱长的最大值为$\sqrt{2}$.分析 在一个棱长为6的正四面体纸盒内放一个正方体,并且能使正方体在纸盒内任意转动,说明正方体在正四面体的内切球内,求出内切球的直径,就是正方体的对角线的长,然后求出正方体的棱长.
解答 解:设球的半径为:r,由正四面体的体积得:
4×$\frac{1}{3}$×r×$\frac{\sqrt{3}}{4}$×62=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×62×$\sqrt{{6}^{2}-(\frac{2}{3}×\frac{\sqrt{3}}{2}×6)^{2}}$,
∴r=$\frac{\sqrt{6}}{2}$,
设正方体的最大棱长为a,
∴3a2=($\sqrt{6}$)2,
∴a=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题是中档题,考查正四面体的内接球的知识,球的内接正方体的棱长的求法,考查空间想象能力,转化思想,计算能力.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.设全集U={0,1,2,3,4},集合A={1,2,3},B={2,3,4},则A∪(∁∪B)=( )
| A. | {0,1,2,3} | B. | {1} | C. | {0,1} | D. | {0} |
19.已知函数f(x)=ex-x2(x<0)与g(x)=x2-ln(a-x)的图象上存在关于x轴的对称点,则a的取值范围为( )
| A. | (-∞,e) | B. | $({-∞,\frac{1}{e}})$ | C. | (-∞,2e) | D. | $({-∞,\frac{1}{2e}})$ |
6.如图,在正方体ABCD-A1B1C1D1中,M为BB1的中点,则二面角M-CD1-A的余弦值为( )
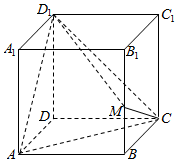

| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
 如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点
如图所示的几何体中,四边形ABCD和四边形BCEF是全等的等腰梯形,且平面BCEF⊥平面ABCD,AB∥DC,CE∥BF,AD=BC,AB=2CD,∠ABC=∠CBF=60°,G为线段AB的中点