题目内容
2.已知命题p:?x∈R,cosx=$\frac{5}{4}$;命题q:?x∈R,2x+1>0.则下列正确的是( )| A. | p∧q是真命题 | B. | p∧(﹁q)是真命题 | C. | ﹁p∧q是真命题 | D. | ﹁p∧﹁q是假命题 |
分析 先判断出p,q的真假,从而判断出复合命题的真假.
解答 解:命题p:?x∈R,cosx=$\frac{5}{4}$,是假命题;
命题q:?x∈R,2x+1>0,是真命题,
故¬p∧q是真命题,
故选:C.
点评 本题考查了复合命题的判断,考查三角函数以及指数函数的性质,是一道基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
10. 已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )
已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )
 已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )
已知函数f(x)的定义域为R,f(-1)=f(2)=1,其导数f′(x)的图象如图所示,设实数x,y满足$\left\{\begin{array}{l}{xy≥0}\\{f(2x+y)≤1}\end{array}\right.$则表达式z=3x+y的最小值为( )| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
7.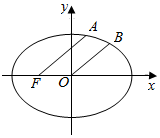 如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
 如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
14.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}<$φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{3}$)=( )


| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
12. 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2019)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2019)的值为( )
 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2019)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2019)的值为( )| A. | $\sqrt{2}$+1 | B. | 2+2$\sqrt{2}$ | C. | 2+$\sqrt{2}$ | D. | -2-2$\sqrt{2}$ |
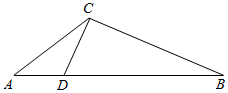 如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,
如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α, 环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.
环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量x,并根据抽检数据绘制了如下图所示的频率分布直方图.