题目内容

5．在正方体ABCD-A1B1C1D1中，E是棱C1D1的中点，则异面直线A1B、EC的夹角的余弦值为（　　）
A．$\frac{{3\sqrt{10}}}{10}$B．$\frac{{\sqrt{10}}}{10}$C．$\frac{{\sqrt{10}}}{5}$D．$\frac{{\sqrt{15}}}{5}$

分析 取A1B1中点F，则BF∥EC，∠A1BF是异面直线A1B、EC的夹角，由此能求出异面直线A1B、EC的夹角的余弦值．

解答 解：取A1B1中点F，则BF∥EC，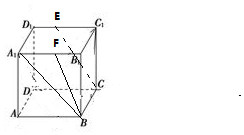
∴∠A1BF是异面直线A1B、EC的夹角，
设正方体ABCD-A1B1C1D1中棱长为2，
则A1F=1，A1B=$\sqrt{4+4}=2\sqrt{2}$，BF=$\sqrt{4+1}=\sqrt{5}$，
∴cos∠A1BF=$\frac{{A}_{1}{B}^{2}+B{F}^{2}-{A}_{1}{F}^{2}}{2{A}_{1}B•BF}$=$\frac{8+5-1}{2×2\sqrt{2}×\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$．
故选：A．

点评 本题考查异面直线所成角的余弦值的求法，是中档题，解题时要认真审题，注意余弦定理的合理运用．

练习册系列答案
相关题目
15．已知三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且PA=2，PB=$\sqrt{3}$，PC=3，则这个三棱锥的外接球的表面积为（　　）
A．16πB．32πC．36πD．64π
16．向量（3，4）在向量（1，2）上的投影为$\frac{11\sqrt{5}}{5}$．
13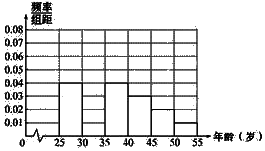．我校高二同学利用暑假进行了社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
组　数分　组低碳族的人数占本组的频率
第一组[25，30）1200.6
第二组[30，35）195p
第三组[35，40）1000.5
第四组[40，45）a0.4
第五组[45，50）300.3
第六组[50，55]150.3
（1）请你补全频率分布直方图，并求出n，a，p的值；
（2）请你利用频率分布直方图估计本次调查人群的年龄的中位数．
20．若f（x）是定义在（0，+∞）上的增函数，且f（$\frac{x}{y}$）=f（x）-f（y）．
（Ⅰ）求f（1）的值；
（Ⅱ）解不等式：f（x-1）＜0．
10．已知集合A={x|x2-2x-15＞0}，B={x|x-6＜0}．命题p：“m∈A”；命题q：“m∈B”．
（1）若命题p为真命题，求实数m的取值范围；
（2）若命题“p∨q”和“p∧q”中恰有一个真命题，求实数m的取值范围．
17．直线l：4x-y-6=0交双曲线x2-$\frac{{y}^{2}}{4}$=1于A，B两点，则线段AB的长为$\frac{2\sqrt{102}}{3}$．
14．已知点F1，F2为椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$的两个焦点，过F1的直线交椭圆于A，B两点，且|AB|=8，则|AF2|+|BF2|=（　　）
A．20B．18C．12D．10
9．已知$a={5^{{{log}_2}3.4}}$，$b={5^{{{log}_3}\frac{10}{3}}}$，c=${（{\frac{1}{5}}）^{{{log}_2}0.3}}$，则（　　）
A．a＞b＞cB．b＞a＞cC．a＞c＞bD．c＞a＞b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网