题目内容
设
，
是平面内一组基底，证明：当λ1
+λ2
=0时，恒有λ1=λ2=0成立．
| e1 |
| e2 |
| e1 |
| e2 |
考点：平面的基本性质及推论
专题：平面向量及应用
分析：利用反证明法证明．
解答：
证明：∵
，
是平面内一组基底，∴
，
不共线，
假设λ1≠λ2≠0，
由题干得：
=-（
）
，∴
，
共线，
与已知条件矛盾，
∴假设不成立，
∴当λ1
+λ2
=0时，恒有λ1=λ2=0成立．
| e1 |
| e2 |
| e1 |
| e2 |
假设λ1≠λ2≠0，
由题干得：
| e1 |
| λ2 |
| λ1 |
| e2 |
| e1 |
| e2 |
与已知条件矛盾，
∴假设不成立，
∴当λ1
| e1 |
| e2 |
点评：本题考查两实数同时等于0的证明，解题时要认真审题，要注意向量知识的灵活运用，是基础题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
若直线l不平行于平面 α，且l?α，则（ ）
| A、α内不存在与l平行的直线 |
| B、α内的所有直线与l异面 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
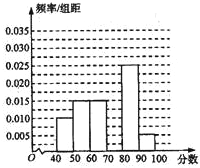某校高一年级有2000名学生，从中随机抽出60名学生，将这60名学生的某次数学考试成绩（百分制）分成六段[40，50），[50，60），…，[90，100]后，得到如图所示的频率分布直方图，观察图形的信息，回答下列问题：
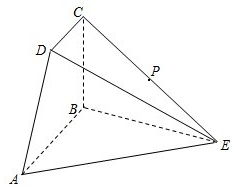如图所示，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，△ABE为等边三角形，且平面ABCD⊥平面ABE，AB=2CD=2BC=2，P为CE中点．