题目内容
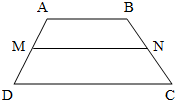用向量法证明：梯形的中位线平行于两底边且等于两底边和的一半．考点：平行向量与共线向量
专题：平面向量及应用
分析：由题意结合所给的图形可得
=
+
+
①，
=
+
+
②，且
+
=
，
+
=
，AB∥CD．①②相加可得
=
，命题得证．
| MN |
| MA |
| AB |
| BN |
| MN |
| MD |
| DC |
| CN |
| MA |
| MD |
| 0 |
| NB |
| NC |
| 0 |
| MN |
| ||||
| 2 |
解答：
证明：如题中的图形所示：由题意可得M、N是梯形ABCD的两腰AD、BC的中点，
∴
=
+
+
①，
=
+
+
②，且
+
=
，
+
=
，AB∥CD．
①②相加可得 2
=
+
，即
=
，
故梯形的中位线平行于两底边且等于两底边和的一半．
∴
| MN |
| MA |
| AB |
| BN |
| MN |
| MD |
| DC |
| CN |
| MA |
| MD |
| 0 |
| NB |
| NC |
| 0 |
①②相加可得 2
| MN |
| AB |
| DC |
| MN |
| ||||
| 2 |
故梯形的中位线平行于两底边且等于两底边和的一半．
点评：本题主要考查梯形的性质，两个向量的加减法及其几何意义，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目