题目内容
12.求下列函数的定义域.(I)y=1g(sinx)+$\sqrt{16-{x}^{2}}$;
(Ⅱ)y=$\sqrt{sinx}$+$\sqrt{tanx}$.
分析 (Ⅰ)直接由根式内部的代数式大于等于0,结合对数函数的性质求解三角不等式得答案;
(Ⅱ)由分子根式内部的代数式大于等于0,联立不等式组求得x的取值集合得答案.
解答 解:(Ⅰ)由题意得:$\left\{\begin{array}{l}{sinx>0}\\{16{-x}^{2}≥0}\end{array}\right.$,
解得:0<x<π,
故函数的定义域是(0,π);
(Ⅱ)要使原函数有意义,则 $\left\{\begin{array}{l}{sinx≥0①}\\{tanx≥0②}\end{array}\right.$,
解①得:2kπ≤x≤2kπ+π,k∈Z;
解②得:kπ≤x<kπ+$\frac{π}{2}$,k∈Z.
取交集得:2kπ≤x<2kπ+$\frac{π}{2}$,或x=(2k+1)π,k∈Z
∴函数的定义域为:{x|2kπ≤x<2kπ+$\frac{π}{2}$或x=(2k+1)π,k∈Z}.
点评 本题考查了函数的定义域及其求法,考查了三角不等式的解法,是基础题.

练习册系列答案
相关题目
20.若α,β均为锐角且α+β>$\frac{π}{2}$,则( )
| A. | sinα>cosβ | B. | sinα<cosβ | C. | sinα>sinβ | D. | sinα<sinβ |
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-a,x≤0}\\{{x}^{2}-3ax+a,x>0}\end{array}\right.$有三个不同的零点,则实数a的取值范围是( )
| A. | ($\frac{4}{9}$,1] | B. | [$\frac{4}{9}$,1] | C. | ($\frac{4}{9}$,+∞) | D. | (0,1] |
4.在等差数列{an}中,前n项和为Sn,且S2013=-2013,a1008=3,则S2014等于( )
| A. | 2014 | B. | -2014 | C. | 1007 | D. | -1007 |
17.某几何体的三视图如图所示,该几何体的侧面积( )
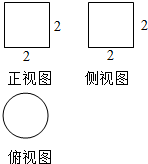

| A. | 5π | B. | 4π | C. | 3π | D. | 2π |