题目内容
20．已知a＞0，b＞0，$a+b=\frac{1}{a}+\frac{1}{b}$，则$\frac{1}{a}+\frac{2}{b}$的最小值为（ ）| A． | 4 | B． | $2\sqrt{2}$ | C． | 8 | D． | 16 |
分析 先求出ab=1，从而求出$\frac{1}{a}+\frac{2}{b}$的最小值即可．
解答 解：由$a+b=\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$，有ab=1，
则$\frac{1}{a}+\frac{2}{b}$$≥2\sqrt{\frac{1}{a}×\frac{2}{b}}=2\sqrt{2}$，
故选：B．
点评 本题考查了基本不等式的性质，是一道基础题．
练习册系列答案
相关题目
10．
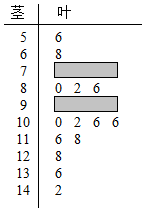某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
（Ⅰ）求表中a，b的值及成绩在[90，110）范围内的个体数；
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．
某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．
15．设x是虚数单位，如果复数$\frac{a+i}{2-i}$的实部与虚部相等，那么实数a的值为（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | 3 | D． | -3 |
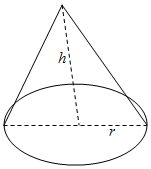如图，某边路清扫机构为预备融化道路积雪，需要在冬天储备$\frac{500}{3}$π（m3）的工业食盐，其食盐堆成底面半径为r（m），高为h（m）的圆锥，并用防水材料S（m2）遮蔽食盐（不考虑接缝与重叠，即面积与圆锥侧面积相同）