题目内容
18．已知△ABC的周长为$\sqrt{2}$+1，且sinA+sinB=$\sqrt{2}$sinC，则边AB的长为1．分析 由题意及正弦定理，得 AB+BC+AC=$\sqrt{2}$+1以及BC+AC=$\sqrt{2}$AB，两式相减，可得AB的值．
解答 解：由题意及正弦定理，得：AB+BC+AC=$\sqrt{2}$+1．
BC+AC=$\sqrt{2}$AB，
两式相减，可得AB=1．
故答案为：1．
点评 本题主要考查正弦定理在解三角形中的应用，属于基础题．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
6．已知函数f（x）的定义域为（-∞，+∞），如果，f（x+2016）=$\left\{\begin{array}{l}\sqrt{2}sinx，x≥0\\ lg（-x），x＜0\end{array}\right.$，那么$f（2016+\frac{π}{4}）•f（-7984）$=（ ）
| A． | 2016 | B． | $\frac{1}{4}$ | C． | 4 | D． | $\frac{1}{2016}$ |
13．若A={x|x2+2x-8＜0}，B={x|x＜1}，则图中阴影部分表示的集合为（ ）
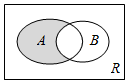
| A． | （-4，1] | B． | （1，2） | C． | [1，2） | D． | （-4，1） |
10．
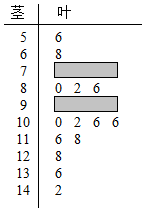某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：
（Ⅰ）求表中a，b的值及成绩在[90，110）范围内的个体数；
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．
某校高三期中考试后，数学教师对本次全部数学成绩按1：20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如表所示的频率分布表：| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150） | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
（Ⅱ）从样本中成绩在[100，130）内的个体中随机抽取4个个体，设其中成绩在[100，110）内的个体数为X，求X的分布列及数学期望E（X）；
（Ⅲ）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取3个，求其中恰好有1个成绩及格的概率（成绩在[90，150）内为及格）．
附注：假定逐次抽取，且各次抽取互相独立．