题目内容
20.在△ABC中,角A,B,C的对边分别为a,b,c,且b=c,2sinB=$\sqrt{3}$sinA.(Ⅰ)求cosB的值;
(Ⅱ)若a=2,求△ABC的面积.
分析 (Ⅰ)因为$2sinB=\sqrt{3}sinA$,所以$2b=\sqrt{3}a$,利用余弦定理求cosB的值;
(Ⅱ)若a=2,求出b,c,sinB,利用三角形面积公式求△ABC的面积.
解答 解:(Ⅰ)因为$2sinB=\sqrt{3}sinA$,所以$2b=\sqrt{3}a$.
所以$a=\frac{2b}{{\sqrt{3}}}$.
所以$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{{{(\frac{2b}{{\sqrt{3}}})}^2}+{b^2}-{b^2}}}{{2×\frac{2b}{{\sqrt{3}}}•b}}=\frac{{\sqrt{3}}}{3}$. …(7分)
(Ⅱ)因为a=2,所以$b=c=\sqrt{3}$.
又因为$cosB=\frac{{\sqrt{3}}}{3}$,所以$sinB=\frac{{\sqrt{6}}}{3}$.
所以S△ABC=$\frac{1}{2}×2×\sqrt{3}×\frac{\sqrt{6}}{3}$=$\sqrt{2}$. …(13分)
点评 本题考查正弦定理、余弦定理的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
11.已知复数z满足z(1-i)2=1+i (i为虚数单位),则|z|为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
12.集合A={x|x2-2x<0},B={x|x-2<0},则( )
| A. | A∩B=∅ | B. | A∩B=A | C. | A∪B=A | D. | A∪B=R |
9.将函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{3}$个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在$[{0,\frac{π}{2}}]$的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
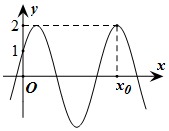 已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.