题目内容
15.设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_n}{a_{n+1}}}}$,若{bn}的前n项和为Tn,证明:Tn<$\frac{1}{2}$.
分析 (1)利用等差数列的通项公式性质及其求和公式即可得出.
(2)利用裂项求和、数列的单调性即可得出.
解答 解:(1)∵{an}等差数列,
由S9=9a5=81,得a5=9.
又由a3+a5=14,得a3=5.
由上可得等差数列{an}的公差d=2.
∴an=a3+(n-3)d=2n-1.
(2)证明:由${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({2n-1})({2n+1})}}=\frac{1}{2}({\frac{1}{{({2n-1})}}-\frac{1}{{({2n+1})}}})$.
得${T_n}=\frac{1}{2}({1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1}})=\frac{1}{2}({1-\frac{1}{2n+1}})<\frac{1}{2}$.
点评 本题考查了等差数列的通项公式性质及其求和公式、裂项求和、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.设复数z满足(1-i)z=|1+$\sqrt{3}i}$|(i为虚数单位),则$\overline z$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.抛物线x2=4y的焦点为F,过F作斜率为$\frac{{\sqrt{3}}}{3}$的直线l与抛物线在y轴右侧的部分相交于点A,过A作抛物线准线的垂线,垂足为H,则△AHF的面积是( )
| A. | 4 | B. | $3\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | 8 |
7.设函数g(x)=ex+3x-a(a∈R,e为自然对数底数),若存在x0∈(-∞,1],使g(g(x0))=x0,则实数a的取值范围为( )
| A. | (-∞,$\sqrt{e}$+$\frac{1}{2}$] | B. | (-∞,e+2] | C. | (-∞,e+$\frac{1}{2}$] | D. | (-∞,$\sqrt{e}$+2] |
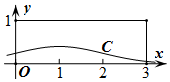 在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )
在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为( )