题目内容
10.记f(n)为最接近$\sqrt{n}$(n∈N*)的整数,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若$\frac{1}{f(1)}$+$\frac{1}{f(2)}$+$\frac{1}{f(3)}$+…+$\frac{1}{f(m)}$=4054,则正整数m的值为( )| A. | 2016×2017 | B. | 20172 | C. | 2017×2018 | D. | 2018×2019 |
分析 写出前几项,找出规律,即可求得m的值.
解答 解:由$\frac{1}{f(1)}$=1,$\frac{1}{f(2)}$=1,2个
$\frac{1}{f(3)}$=$\frac{1}{2}$,$\frac{1}{f(4)}$=$\frac{1}{2}$,$\frac{1}{f(5)}$=$\frac{1}{2}$,$\frac{1}{f(6)}$=$\frac{1}{2}$,4个
$\frac{1}{f(7)}$=$\frac{1}{3}$,$\frac{1}{f(8)}$=$\frac{1}{3}$,$\frac{1}{f(9)}$=$\frac{1}{3}$,$\frac{1}{f(10)}$=$\frac{1}{3}$,$\frac{1}{f(11)}$=$\frac{1}{3}$,$\frac{1}{f(12)}$=$\frac{1}{3}$,6个
$\frac{1}{f(13)}$=$\frac{1}{4}$,$\frac{1}{f(14)}$=$\frac{1}{4}$,…$\frac{1}{f(20)}$=$\frac{1}{4}$,8个
…
∴…$\frac{1}{f[m×(m+1)]}$=$\frac{1}{m}$,
∴$\frac{1}{f(1)}$+$\frac{1}{f(2)}$+$\frac{1}{f(3)}$+…+$\frac{1}{f(m)}$=1×2+$\frac{1}{2}$×4+$\frac{1}{3}$×6+…+$\frac{1}{n}$×2n=4034,
则$\stackrel{n}{\overbrace{2+2+2+…+2}}$=4034,则2n=4034,则n=2017,
∴总共有2017个$\frac{1}{2017}$,
则$\frac{1}{f(m)}$=$\frac{1}{2017×2018}$,
故m的值为2017×2018;
故选C.
点评 本题考查函数值的求法,要求学生通过观察,分析归纳发现规律的能力,考查学生分析问题及解决问题的能力,属于中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | ac2>bc2 | C. | 2-a<2-b | D. | lga>lgb |
| A. | -7 | B. | -8 | C. | -22 | D. | 27 |
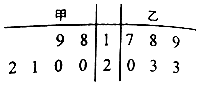 甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.
甲、乙两名技工在相同的条件下生产某种零件,连续6天中,他们日加工的合格零件数的统计数据的茎叶图,如图所示.