题目内容
己知函数 .
.
(I)求 的极大值和极小值;
的极大值和极小值;
(II)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(I) 的极大值为
的极大值为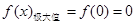 和
和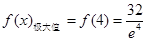 ;
; 的极小值为
的极小值为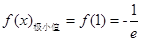 .(II)
.(II) 的取值范围是
的取值范围是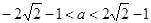 .
.
解析试题分析:(I) 易知函数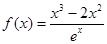 定义域为
定义域为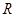 ,在
,在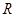 上讨论
上讨论 的极值先求导
的极值先求导 ,列出
,列出 的正负表,再根据函数的单调性和极值与倒数的关系即可求出极值.
的正负表,再根据函数的单调性和极值与倒数的关系即可求出极值.
(II) 本题是不等式恒成立求参数范围问题,一般思路是化简-分类讨论,但本题中化简后为 ,如果用
,如果用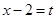 即
即 换元后为
换元后为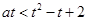 讨论起来更简单.分别讨论?
讨论起来更简单.分别讨论?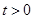 时,化简为
时,化简为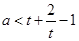 ;?
;?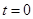 时,恒成立;?
时,恒成立;?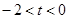 时化简为
时化简为 三种情况,运用均值不等式求出范围即可.
三种情况,运用均值不等式求出范围即可.
试题解析:(I) 函数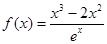 ,知定义域为
,知定义域为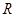 ,
, .
.
所以 的变化情况如下:
的变化情况如下:








+ 0 - 0 + 0 - 
递增 极大值 递减 极小值  练习册系列答案
练习册系列答案
名题文化步步高书系名题系列答案
倍速训练法一练通系列答案
金牌教辅夺冠金卷系列答案
海淀名师名校百分卷系列答案
8848高中同步学情跟进卷系列答案
中考实战名校在招手系列答案

伴你学山西系列答案

新学案综合课课练系列答案
相关题目
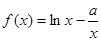 (
(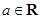 ).
).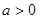 时,判断
时,判断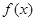 在定义域上的单调性;
在定义域上的单调性;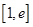 上的最小值为
上的最小值为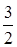 ,求
,求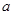 的值;
的值;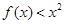 在
在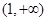 上恒成立,试求
上恒成立,试求 .
. 的最小正周期和最小值;
的最小正周期和最小值; 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (其中
(其中 为常数).
为常数). 时,求函数的单调区间;
时,求函数的单调区间;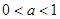 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且 .证明:
.证明: .
. ,其中
,其中 .
. 时判断
时判断 的单调性;
的单调性; 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数 的取值范围;
的取值范围; ,当
,当 时,若
时,若 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.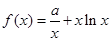 ,
,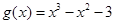 .
.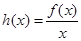 的单调性;
的单调性;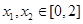 ,使得
,使得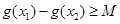 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数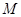 ;
;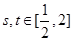 ,都有
,都有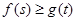 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
.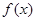 的单调区间和极值;
的单调区间和极值;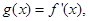 直线
直线 与曲线
与曲线 相交于
相交于 不同两点,若
不同两点,若 试证明
试证明 .
. ,
, .
. 的单调递增区间;
的单调递增区间; 为函数
为函数 处的切线的斜率恒大于
处的切线的斜率恒大于 ,
, 的取值范围.
的取值范围. ,
, .
. 为
为 的导函数,若不等式
的导函数,若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立,求m(m∈Z,m
恒成立,求m(m∈Z,m 1)的值.
1)的值.