题目内容
已知函数 (其中
(其中 为常数).
为常数).
(Ⅰ)当 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)当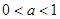 时,设函数
时,设函数 的3个极值点为
的3个极值点为 ,且
,且 .证明:
.证明: .
.
(Ⅰ)单调减区间为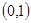 ,
,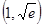 ;增区间为
;增区间为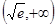 .(Ⅱ)详见解析.
.(Ⅱ)详见解析.
解析试题分析:(Ⅰ)将 代入
代入 ,然后求导便可得其单调区间.
,然后求导便可得其单调区间.
(Ⅱ)我们分以下几步来分析.
第一步、对 求导得:
求导得: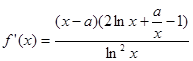 .显然
.显然 是它的一个极值点,下面我们要弄清楚
是它的一个极值点,下面我们要弄清楚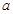 应该是
应该是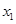 还是
还是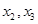 .另两个极值点便是方程
.另两个极值点便是方程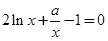 的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数
的根.对这个方程,我们不可能直接解,所以接下来就利用导数研究函数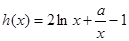 .
.
第二步、对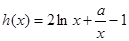 求导得:
求导得: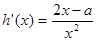
∴函数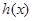 在
在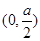 上单调递减,在
上单调递减,在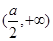 上单调递增
上单调递增
当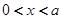 时,
时,
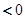 ,
,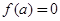 .又
.又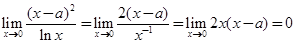 ,
,
所以 在
在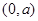 上必有一个极值点.
上必有一个极值点.
因为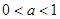 ,所以
,所以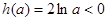 ,
,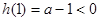 ,
,
∴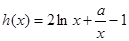 的两个零点必有一个小于
的两个零点必有一个小于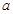 (实际上比
(实际上比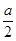 还小),而另一个大于1,
还小),而另一个大于1,
∴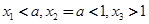 .
.
∴当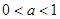 时,
时,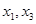 是函数
是函数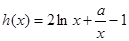 的两个零点,且
的两个零点,且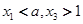 .
.
即有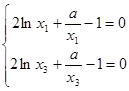 .这样问题转化为在该条件下证明
.这样问题转化为在该条件下证明 .那么这个不等式如何证呢?
.那么这个不等式如何证呢?
第三步、注意到待证不等式 中不含
中不含 ,故考虑消去
,故考虑消去 ,找到
,找到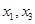 之间的关系式.
之间的关系式.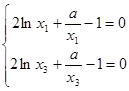 消去
消去 有
有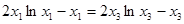 .
.
令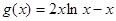 ,
,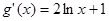 有零点
有零点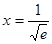 .
.
∴函数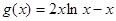 在
在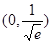 上递减,在
上递减,在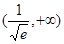 上递增,
上递增,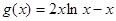 在
在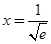 处取得极小值.由于
处取得极小值.由于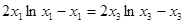 ,所以
,所以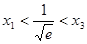 .
.
因为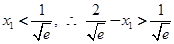 .
.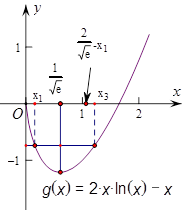
所以要证明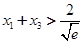 ,只需证
,只需证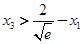 .那么这个不等式又如何证明呢?
.那么这个不等式又如何证明呢?
因为函数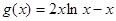 在
在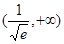 上递增,所以转化为证
上递增,所以转化为证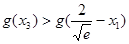 .
. 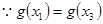
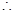 即证
即证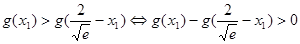 .
.
这个不等式,通过构造函数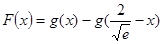 ,再利用导数就很容易证明了.
,再利用导数就很容易证明了.
试题解析:(Ⅰ)求导得: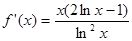 .
.
令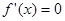 可得
可得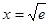 .列表如下:
.列表如下:
金博优题典单元练测活页卷系列答案
DIY英语系列答案
晨光全优口算应用题天天练系列答案
提优检测卷初中强化拓展系列答案
百渡中考必备中考试题精选系列答案
魅力语文系列答案
状元龙初中语文现代文阅读系列答案
初中现代文文言文拓展阅读系列答案
启光中考全程复习方案系列答案
授之以渔中考试题汇编系列答案
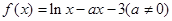
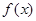 的单调性;
的单调性;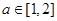 ,若函数
,若函数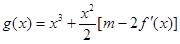 在 区间
在 区间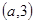 上有最值,求实数
上有最值,求实数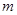 的取值范围.
的取值范围. +
+ ,g(x)=
,g(x)= ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数) }中,a1=1,
}中,a1=1,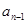 )(n≥2),求证:
)(n≥2),求证: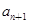 <
< <
< .
. 和
和 是函数
是函数 的两个极值点,其中
的两个极值点,其中 ,
, .
. 的取值范围;
的取值范围; ,求
,求 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底. ,(
,( 且
且 ).
). ,令
,令 ,试判断函数
,试判断函数 在
在 上的单调性并证明你的结论;
上的单调性并证明你的结论; 且
且
 的定义域和值域都是
的定义域和值域都是 的最大值;
的最大值; 对
对 恒成立,求实数
恒成立,求实数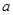 的取值范围;
的取值范围;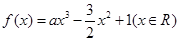 ,其中
,其中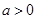 .
. ,求曲线
,求曲线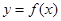 在点
在点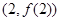 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围. .
. 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的图像过原点,
的图像过原点, ,
, 的导函数为
的导函数为 ,且
,且 ,
,

 ,
, 的解析式;
的解析式; 的极小值;
的极小值; 和
和 ,使得
,使得 和
和 若存在,求出
若存在,求出
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 的取值范围.
的取值范围.