题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,a2=b2+c2+bc.
(1)求角A的大小;
(2)若a=2
,b=2,求c的值.
(1)求角A的大小;
(2)若a=2
| 2 |
考点:余弦定理
专题:解三角形
分析:(1)由a2=b2+c2+bc得b2+c2-a2=-bc,根据余弦定理求出cosA的值,再求角A的值;
(2)把a=2
,b=2,A=120°代入a2=b2+c2-2bccosA,化简后根据一元二次方程的解法求出c的值.
(2)把a=2
| 2 |
解答:
解:(1)由a2=b2+c2+bc得,b2+c2-a2=-bc,
则cosA=
=-
,
∵0°<A<180°,∴A=120°,
(2)∵a=2
,b=2,A=120°,
由余弦定理得,a2=b2+c2-2bccosA,
∴8=4+c2-4ccos120°,即c2+2c-4=0,
解得,c=-1+
或c=-1-
(舍去),
则c的值是-1+
.
则cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∵0°<A<180°,∴A=120°,
(2)∵a=2
| 2 |
由余弦定理得,a2=b2+c2-2bccosA,
∴8=4+c2-4ccos120°,即c2+2c-4=0,
解得,c=-1+
| 5 |
| 5 |
则c的值是-1+
| 5 |
点评:本题考查余弦定理的应用,特殊角的三角函数值,熟练掌握公式并会应用是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
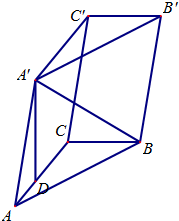 如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.
如图,三棱柱ABC-A′B′C′中,点A′在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC′=2.