题目内容
7.函数y=1-$\frac{2}{{4}^{x}+1}$的值域为( )| A. | (-∞,-1) | B. | (-∞,-1] | C. | [-1,1] | D. | (-1,1) |
分析 由4x>0便可求出4x+1的范围,进而求出$\frac{1}{{4}^{x}+1}$的范围,从而得出y的范围,即得出原函数的值域.
解答 解:4x>0;
∴4x+1>1;
∴$0<\frac{1}{{4}^{x}+1}<1$;
∴-1<y<1;
∴该函数的值域为(-1,1).
故选:D.
点评 考查函数值域的概念,指数函数的值域,以及根据不等式的性质求函数值域的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若集合A={x|-2≤x≤3},B={x|x<-1或x>4},则集合A∩B等于( )
| A. | {x|-1<x≤3} | B. | {x|-2≤x<-1} | C. | {x|3≤x<4} | D. | {x|x≤3或x>4} |
15. 如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )
如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )
 如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )
如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
2.集合$M=\left\{{1,-1}\right\},N=\left\{{x\left|{\frac{1}{2}}\right.<{2^{x+1}}<4,x∈Z}\right\}$,M∩N=( )
| A. | {-1,1} | B. | {-1} | C. | {0} | D. | {-1,0} |
19.△ABC的三个内角A,B,C对应的边分别为a,b,c,且asin($\frac{3π}{2}$-C),bcos(2π-B),ccos(π+A)成等差数列,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
16.若复数z满足$({1+i})\cdotz=i$,则此复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
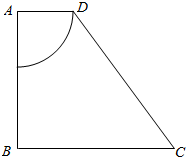 如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.
如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.