题目内容
17.已知函数f(x)=$\frac{6x}{{x}^{2}+1}$.(Ⅰ)判断函数f(x)的奇偶性,并证明你的结论;
(Ⅱ)求满足不等式f(2x)>2x的实数x的取值范围.
分析 (Ⅰ)可看出f(x)为奇函数,求f(x)的定义域为R,且容易得到f(-x)=-f(x),从而证出f(x)为奇函数;
(Ⅱ)由原不等式可以得到$\frac{6•{2}^{x}}{{2}^{2x}+1}>{2}^{x}$,可化简成22x<5,不等式两边取以2为底的对数便可得出实数x的取值范围.
解答 解:(Ⅰ)f(x)为奇函数,证明如下:
f(x)的定义域为R,f(-x)=$\frac{-6x}{{x}^{2}+1}=-f(x)$;
∴f(x)为奇函数;
(Ⅱ)由f(2x)>2x得,$\frac{6•{2}^{x}}{{2}^{2x}+1}>{2}^{x}$;
∴$\frac{6}{{2}^{2x}+1}>1$;
整理成22x<5;
∴2x<log25;
∴$x<\frac{lo{g}_{2}5}{2}$;
即$x<lo{g}_{2}\sqrt{5}$;
∴实数x的取值范围为(-∞,$lo{g}_{2}\sqrt{5}$).
点评 考查奇函数的定义及判断方法和过程,指数函数的值域,分式不等式的解法,以及指数式和对数式的互化,对数函数的单调性.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
7.函数y=1-$\frac{2}{{4}^{x}+1}$的值域为( )
| A. | (-∞,-1) | B. | (-∞,-1] | C. | [-1,1] | D. | (-1,1) |
2.某校高一学生1500人,高二学生1200人,高三学生1300人,为了调查高中各年级学生的寒假学习计划,决定采用分层抽样法抽取200人进行调查,则应从高二年级抽取的人数为( )
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
9.设命题p:?x>1,x+$\frac{1}{x}$>2,则¬p为( )
| A. | ?x>1,x+$\frac{1}{x}$≤2 | B. | ?x>1,x+$\frac{1}{x}$≤2 | C. | ?x≤1,x+$\frac{1}{x}$≤2 | D. | ?x≤1,x+$\frac{1}{x}$≤2 |
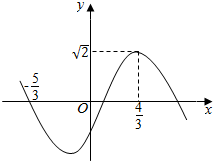 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.