题目内容
已知f(x)=5
cos2x+
sin2x-4sinxcosx.
(1)求f(
);
(2)若f(a)=5
,a∈(
,π),求角a.
| 3 |
| 3 |
(1)求f(
| 5π |
| 12 |
(2)若f(a)=5
| 3 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(1)运用二倍角公式和两角差的正弦公式,以及特殊角的函数值,即可得到;
(2)代入化简计算,再由a的范围,以及特殊角的函数值,即可求得a.
(2)代入化简计算,再由a的范围,以及特殊角的函数值,即可求得a.
解答:
解:(1)f(x)=5
cos2x+
sin2x-4sinxcosx
=
(1+cos2x)+
(1-cos2x)-2sin2x=3
-4(
sin2x-
cos2x)
=3
-4sin(2x-
).
则f(
)=3
-4sin(
-
)=3
-4;
(2)若f(a)=5
,即有3
-4sin(2a-
)=5
,
即sin(2a-
)=-
,
由于a∈(
,π),则2a-
∈(
,
),
即有2a-
=
,
即有a=
.
| 3 |
| 3 |
=
5
| ||
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=3
| 3 |
| π |
| 3 |
则f(
| 5π |
| 12 |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
(2)若f(a)=5
| 3 |
| 3 |
| π |
| 3 |
| 3 |
即sin(2a-
| π |
| 3 |
| ||
| 2 |
由于a∈(
| π |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 3 |
即有2a-
| π |
| 3 |
| 4π |
| 3 |
即有a=
| 5π |
| 6 |
点评:本题考查三角函数的化简和求值,考查二倍角公式和两角差的正弦公式,考查特殊角的三角函数值,考查运算能力,属于中档题.

练习册系列答案
相关题目
某几何体的立体图如图所示,该几何体的三视图不可能是( )
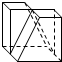

A、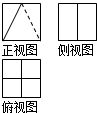 |
B、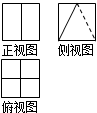 |
C、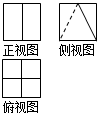 |
D、 |