题目内容
对于函数f(x),若在定义域内存在实数x,使得f(-x)=-f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+4x-a(a∈R),试判断f(x)是否为“局部奇函数”?并说明理由;
(2)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围;
(3)(文)若f(x)=ex-ex-2m为定义域R上的“局部奇函数”,求证:若x>1,则ex>x2-2mx+1.
(1)已知二次函数f(x)=ax2+4x-a(a∈R),试判断f(x)是否为“局部奇函数”?并说明理由;
(2)若f(x)=2x+m是定义在区间[-1,1]上的“局部奇函数”,求实数m的取值范围;
(3)(文)若f(x)=ex-ex-2m为定义域R上的“局部奇函数”,求证:若x>1,则ex>x2-2mx+1.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用局部奇函数的定义,建立方程关系,然后判断方程是否有解即可.
解答:
解:f(x)为“局部奇函数”等价于关于x的方程f(x)+f(-x)=0有解.
(1)当f(x)=ax2+4x-a(a∈R)时,
方程f(x)+f(-x)=0即2a(x2-1)=0有解x=±1,所以f(x)为“局部奇函数”.
(2)当f(x)=2x+m时,f(-x)=-f(x)可化为2x+2-x+2m=0,
因为f(x)的定义域为[-1,1],所以方程2x+2-x+2m=0在[-1,1]上有解.…(5分)
令t=2x∈[
,2],则-2m=t+
.
设g(t)=t+
,则g'(t)=1-
=
,
当t∈(0,1)时,g'(t)<0,故g(t)在(0,1)上为减函数,
当t∈(1,+∞)时,g'(t)>0,故g(t)在(1,+∞)上为增函数. …(7分)
所以t∈[
,2]时,g(t)∈[2,
].
所以-2m∈[2,
],即m∈[-
,-1]. …(9分)
(文)f(x)=ex-ex-2m为定义域R上的“局部奇函数”,
f(x)+f(-x)=0可化为m=
≥
=
(x=0时等号成立),即m≥
.
设g(x)=ex-x2+2mx-1(x>1),由g'(x)=ex-2x+2m≥ex-2x+1,
显然,由图象知,x>1时ex-2x+1>0成立,所以g'(x)≥ex-2x+1>0,
函数g(x)=ex-x2+2mx-1在(1,+∞)上递增,则g(x)>g(1)=e+2m-2≥e+2×
-2>0.
即ex>x2-2mx+1成立.
(1)当f(x)=ax2+4x-a(a∈R)时,
方程f(x)+f(-x)=0即2a(x2-1)=0有解x=±1,所以f(x)为“局部奇函数”.
(2)当f(x)=2x+m时,f(-x)=-f(x)可化为2x+2-x+2m=0,
因为f(x)的定义域为[-1,1],所以方程2x+2-x+2m=0在[-1,1]上有解.…(5分)
令t=2x∈[
| 1 |
| 2 |
| 1 |
| t |
设g(t)=t+
| 1 |
| t |
| 1 |
| t2 |
| t2-1 |
| t2 |
当t∈(0,1)时,g'(t)<0,故g(t)在(0,1)上为减函数,
当t∈(1,+∞)时,g'(t)>0,故g(t)在(1,+∞)上为增函数. …(7分)
所以t∈[
| 1 |
| 2 |
| 5 |
| 2 |
所以-2m∈[2,
| 5 |
| 2 |
| 5 |
| 4 |
(文)f(x)=ex-ex-2m为定义域R上的“局部奇函数”,
f(x)+f(-x)=0可化为m=
| ex+e-x |
| 4 |
2
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
设g(x)=ex-x2+2mx-1(x>1),由g'(x)=ex-2x+2m≥ex-2x+1,
显然,由图象知,x>1时ex-2x+1>0成立,所以g'(x)≥ex-2x+1>0,
函数g(x)=ex-x2+2mx-1在(1,+∞)上递增,则g(x)>g(1)=e+2m-2≥e+2×
| 1 |
| 2 |
即ex>x2-2mx+1成立.
点评:本题主要考查新定义的应用,利用新定义,建立方程关系,然后利用函数性质进行求解是解决本题的关键,考查学生的运算能力.

练习册系列答案
相关题目
某班有50名学生,其中正、副班长各1人,现要选派5人参加一项社区活动,要求正、副班长至少1人参加,问共有多少种选派方法?下面是学生提供的四个计算式,其中错误的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
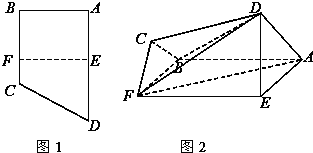 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE. 如图,已知椭圆C:
如图,已知椭圆C: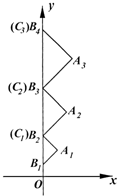 如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).
如图,在直角坐标系xOy中,有一组底边长为an的等腰直角三角形AnBnCn(n=1,2,…),底边BnCn依次放置在y轴上(相邻顶点重合),点B1的坐标为(0,b).