题目内容
在△ABC中,A,B,C所对的边分别为a,b,c,ac=3,S△ABC=
.
(Ⅰ)求B;
(Ⅱ)若b=
,求△ABC的周长.
3
| ||
| 4 |
(Ⅰ)求B;
(Ⅱ)若b=
| 2 |
考点:正弦定理
专题:三角函数的求值,解三角形
分析:(Ⅰ)利用三角形面积公式列出关系式,将ac,已知面积代入求出sinB的值,即可确定出B的度数;
(Ⅱ)利用余弦定理列出关系式,将cosB的值,b,ac的值代入求出a+c的值,即可确定三角形ABC周长.
(Ⅱ)利用余弦定理列出关系式,将cosB的值,b,ac的值代入求出a+c的值,即可确定三角形ABC周长.
解答:
解:(Ⅰ)∵S△ABC=
acsinB=
,ac=3,
∴sinB=
,
∵B为三角形内角,
∴B=
或
;
(Ⅱ)当B=
,b=
,ac=3时,由余弦定理得:b2=a2+c2-2accos
=(a+c)2-3ac,
即2=(a+c)2-9,
解得:a+c=
,
此时△ABC周长为a+b+c=
+
;
当B=
时,b=
,ac=3,由余弦定理得:b2=a2+c2-2accos
=a2+c2+ac,
即2=a2+c2+3,
∴a2+c2=-1(舍去),
综上,△ABC周长为
+
.
| 1 |
| 2 |
3
| ||
| 4 |
∴sinB=
| ||
| 2 |
∵B为三角形内角,
∴B=
| π |
| 3 |
| 2π |
| 3 |
(Ⅱ)当B=
| π |
| 3 |
| 2 |
| π |
| 3 |
即2=(a+c)2-9,
解得:a+c=
| 11 |
此时△ABC周长为a+b+c=
| 11 |
| 2 |
当B=
| 2π |
| 3 |
| 2 |
| 2π |
| 3 |
即2=a2+c2+3,
∴a2+c2=-1(舍去),
综上,△ABC周长为
| 11 |
| 2 |
点评:此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知某算法的流程图如图所示,若输入x=7,y=6,则输出的有序数对为( )
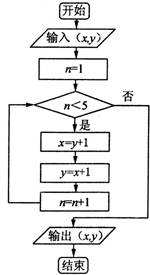

| A、(13,14) |
| B、(12,13) |
| C、(14,13) |
| D、(13,12) |
设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |
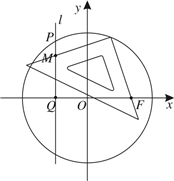 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且