题目内容
己知函数f(x)=-
x3+2ax2-3a2x(a∈R且a≠0).
(Ⅰ)当a=-1时,求曲线y=f(x)在(-2,m)处的切线方程:
(Ⅱ)当a>0时,求函数y=f(x)的单调区间和极值;
(Ⅲ)当x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,求a的取值范围.
| 1 |
| 3 |
(Ⅰ)当a=-1时,求曲线y=f(x)在(-2,m)处的切线方程:
(Ⅱ)当a>0时,求函数y=f(x)的单调区间和极值;
(Ⅲ)当x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,求a的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求出切点坐标,切线斜率,可得曲线y=f(x)在(-2,m)处的切线方程;
(Ⅱ)求导函数,利用导数的正负,可得函数的单调区间,从而可得函数的极值;
(Ⅲ)求出f′(x)在区间[2a,2a+2]上的最大值与最小值,利用当x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,可得
,即可求a的取值范围.
(Ⅱ)求导函数,利用导数的正负,可得函数的单调区间,从而可得函数的极值;
(Ⅲ)求出f′(x)在区间[2a,2a+2]上的最大值与最小值,利用当x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,可得
|
解答:
解:(Ⅰ)当a=-1时,∵函数f(x)=-
x3+2ax2-3a2x(a∈R且a≠0),
∴f′(x)=-x2-4x-3,
∴f′(2)=1,m=f(2)=
,
∴曲线y=f(x)在(-2,m)处的切线方程:y-
=x-2,即3x-3y+8=0;
(Ⅱ)f′(x)=-x2+4ax-3a2=-(x-a)(x-3a),
当a>0时,由f′(x)>0,得a<x<3a;由f′(x)<0,得x<a或x>3a,
∴y=f(x)的增区间为(a,3a),减区间为(-∞,a)和(3a,+∞),
∴x=3a时,函数的极大值为0,x=a时,极小值为-
a3;
(Ⅲ)f′(x)=-x2+4ax-3a2=-(x-2a)2+a2,
∵f′(x)在区间[2a,2a+2]上单调递减,
∴x=2a时,f′(x)max=a2,x=2a+2时,f′(x)min=a2-4,
∵x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,
∴
,
∴1≤a≤3,
∴a的取值范围为[1,3].
| 1 |
| 3 |
∴f′(x)=-x2-4x-3,
∴f′(2)=1,m=f(2)=
| 2 |
| 3 |
∴曲线y=f(x)在(-2,m)处的切线方程:y-
| 2 |
| 3 |
(Ⅱ)f′(x)=-x2+4ax-3a2=-(x-a)(x-3a),
当a>0时,由f′(x)>0,得a<x<3a;由f′(x)<0,得x<a或x>3a,
∴y=f(x)的增区间为(a,3a),减区间为(-∞,a)和(3a,+∞),
∴x=3a时,函数的极大值为0,x=a时,极小值为-
| 4 |
| 3 |
(Ⅲ)f′(x)=-x2+4ax-3a2=-(x-2a)2+a2,
∵f′(x)在区间[2a,2a+2]上单调递减,
∴x=2a时,f′(x)max=a2,x=2a+2时,f′(x)min=a2-4,
∵x∈[2a,2a+2]时,不等式|f′(x)|≤3a恒成立,
∴
|
∴1≤a≤3,
∴a的取值范围为[1,3].
点评:本题考查导数知识的综合运用,考查导数是几何意义,考查函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
若P为△ABC内一点,且
+
+2
=
,在△ABC内随机撒一颗豆子,则此豆子落在△PBC内的概率为( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
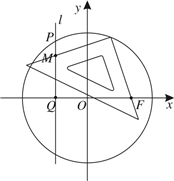 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且