题目内容

19．已知向量$\overrightarrow a=（2，1）$，$\overrightarrow b=（1，1）$，$\overrightarrow c=（5，2）$，$\overrightarrow m=λ\overrightarrow b+\overrightarrow c$（λ为常数）．
（1）求$\overrightarrow a+\overrightarrow b$；
（2）若$\overrightarrow a$与$\overrightarrow m$平行，求实数λ的值．

分析 （1）根据题意，由向量$\overrightarrow{a}$、$\overrightarrow{b}$的坐标，由向量的加法坐标计算公式，计算即可得答案；
（2）根据题意，求出$\overrightarrow{m}$的坐标，由向量平行的坐标表示公式可得2（λ+2）=λ+5，解可得λ的值，即可得答案．

解答 解：（1）因为$\overrightarrow a=（2，1）$，$\overrightarrow b=（1，1）$，所以$\overrightarrow a+\overrightarrow b=（2，1）+（1，1）=（3，2）$．
（2）因为$\overrightarrow b=（1，1）$，$\overrightarrow c=（5，2）$，所以$\overrightarrow m=λ\overrightarrow b+\overrightarrow c=λ（1，1）+（5，2）=（λ+5，λ+2）$．
又因为$\overrightarrow a=（2，1）$，且$\overrightarrow a$与$\overrightarrow m$平行，所以2（λ+2）=λ+5，解得λ=1．

点评 本题考查向量平行的坐标表示，涉及向量的坐标运算，关键是掌握向量坐标计算的公式．

练习册系列答案
相关题目
10．一个几何体的三视图如图所示（其中主视图的弧线为四分之一圆周），则该几何体的体积为（　　）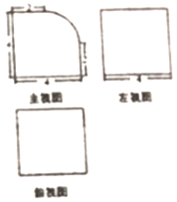
A．64-4πB．64+6πC．48+4πD．64-6π
11．对于函数$f（x）=sin（x+\frac{3π}{2}）cos（\frac{π}{2}+x）$，给出下列四个结论：
（1）函数f（x）的最小正周期为π；    
（2）若f（x1）=-f（x2），则x1=-x2；
（3）f（x）的图象关于直线$x=-\frac{π}{4}$对称；
（4）f（x）在$[{\frac{π}{4}，\frac{3π}{4}}]$上是减函数．
其中正确的个数为（　　）
A．2B．4C．1D．3
7．已知M是抛物线x2=16y上任意一点，A（0，4），B（-1，1），则|MA|+|MB|的最小值为（　　）
A．$\sqrt{10}$B．3C．8D．5
14．若函数f（x）=e-x+1，则f′（1）=-1．
4．已知抛物线的顶点在坐标原点，对称轴是x轴，顶点与焦点的距离等于4．
（1）求抛物线的方程
（2）若等边三角形的一个顶点位于原点，另外两个顶点在抛物线上，求这个等边三角形的边长．
11．定义min$\left\{{a，b}\right\}=\left\{{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}}$，若实数x，y满足$\left\{{\begin{array}{l}{x-y-3≤0}\\{3x-y-9≥0}\\{y≤3}\end{array}}$，设z=min{2x-y+4，x+y+6}，则z的取值范围是（　　）
A．[9，11]B．[9，12]C．[9，13]D．[9，14]
8．函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，
（1）求函数f（x）的解析式；
（2）求f（-$\frac{5π}{3}$）的值．
9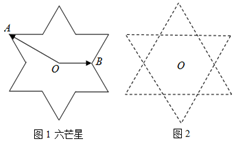．如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（　　）
A．[-4，4]B．$[{-\sqrt{21}，\sqrt{21}}]$C．[-5，5]D．[-6，6]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网