题目内容

16．等差数列{an}的前n项和是Sn，若a1+a2=5，a5+a6=13，则S6的值为（　　）
A．18B．27C．36D．46

分析 利用等差数列的通项公式及其前n项和公式即可得出．

解答 解：设等差数列{an}的公差为d，∵a1+a2=5，a5+a6=13，
∴$\left\{\begin{array}{l}{2{a}_{1}+d=5}\\{2{a}_{1}+9d=13}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=1}\end{array}\right.$，
则S6=6×2+$\frac{6×5}{2}$×1=27．
故选：B．

点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．直线y=2x+b能否与函数f（x）=sinx相切？说明你的理由．
9．利用定积分的几何意义计算．
（1）${∫}_{-1}^{1}$xdx；
（2）${∫}_{-R}^{R}$$\sqrt{{R}^{2}{-x}^{2}}dx$．
4．某地区有高中学校10所、初中学校30所，小学学校60所，现采用分层抽样的方法从这些学校中抽取20所学校对学生进行体质健康检查，则应抽取初中学校6所．
11．已知全集U=R，集合A={x|x+1≥1且x-3≤0}，B={x|a≤x≤a+2，a∈R}．
（1）当a=1时，求A∩B；
（2）当集合A，B满足B⊆A时，求实数a取值范围．
1．已知函数f（x）=2x+2x-6的零点为x0，那么x0所在的区间是（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
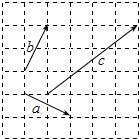8．如图，在6×6的方格中，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$的起点和终点均在格点，且满足向量$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$（x，y∈R），那么x+y=3．
5．已知函数$f（x）=\frac{{\sqrt{4x+5-{x^2}}}}{x+1}$的定义域为集合A，函数g（x）=lg（-x2+2x+m）的定义域为集合B．
（Ⅰ）当m=3时，求A∩∁RB；
（Ⅱ）若A∩B={x|-1＜x＜4}，求实数m的值．
6．已知集合P={1，3，5，7}，Q={x|2x-1＞5}，则P∩Q等于（　　）
A．{7}B．{5，7}C．{3，5，7}D．{x|3＜x≤7}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网