题目内容
5.已知函数$f(x)=\frac{{\sqrt{4x+5-{x^2}}}}{x+1}$的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.(Ⅰ)当m=3时,求A∩∁RB;
(Ⅱ)若A∩B={x|-1<x<4},求实数m的值.
分析 (Ⅰ)先化简集合A,B,再根据补集和交集的定义即可求出;
(Ⅱ)根据交集的定义即可求出m的范围.
解答 解:(Ⅰ)由$f(x)=\frac{{\sqrt{4x+5-{x^2}}}}{x+1}$的定义域得A={x|-1<x≤5}.
当m=3时,B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3}.
所以A∩∁RB={x|3≤x≤5}.
(Ⅱ)因为A={x|-1<x≤5},A∩B={x|-1<x<4},
所以有-42+2×4+m=0.
解得m=8.
此时B={x|-2<x<4},符合题意.
所以m=8.
点评 本题考查了函数的定义域的求法和集合的基本运算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.等差数列{an}的前n项和是Sn,若a1+a2=5,a5+a6=13,则S6的值为( )
| A. | 18 | B. | 27 | C. | 36 | D. | 46 |
13.经过点A(2,3)和点B(4,7)的直线方程是( )
| A. | 2x+y-7=0 | B. | 2x-y+1=0 | C. | 2x-y-1=0 | D. | -2y+4=0 |
10.已知$cos(θ+\frac{π}{6})=-\frac{{\sqrt{3}}}{3}$,则$sin(\frac{π}{6}-2θ)$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
17.已知集合A={0,1,2},B={2,3},则集合A∪B=( )
| A. | {1,2,3} | B. | {0,1,2,3} | C. | {2} | D. | {0,1,3} |
14.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,2),k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$平行,则k的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
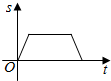 如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )