题目内容
11.若$\int_0^1{({x^2}+mx)}dx=0$,则实数m的值为-$\frac{2}{3}$.分析 根据定积分的计算法则计算即可.
解答 解:${∫}_{0}^{1}$(x2+mx)dx=($\frac{1}{3}{x}^{3}$+$\frac{1}{2}$mx2)|${\;}_{0}^{1}$=$\frac{1}{3}$+$\frac{1}{2}$m=0,
∴m=-$\frac{2}{3}$,
故答案为:-$\frac{2}{3}$
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
1.已知O为△ABC内一点,且有$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$,记△ABC,△BCO,△ACO的面积分别为S1,S2,S3,则S1:S2:S3等于( )
| A. | 3:2:1 | B. | 3:1:2 | C. | 6:1:2 | D. | 6:2:1 |
19.设a为实数,函数f(x)=x3+ax2+(a-3)x的导函数f′(x),且f′(x)是偶函数,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| A. | 9x+y+16=0 | B. | 9x-y-16=0 | C. | 9x-y+16=0 | D. | 9x+y-16=0 |
20.已知数据x1,x2,x3,…,x50,500(单位:公斤),其中x1,x2,x3,…,x50,是某班50个学生的体重,设这50个学生体重的平均数为x,中位数为y,则x1,x2,x3,…,x50,500这51个数据的平均数、中位数分别与x、y比较,下列说法正确的是( )
| A. | 平均数增大,中位数一定变大 | B. | 平均数增大,中位数可能不变 | ||
| C. | 平均数可能不变,中位数可能不变 | D. | 平均数可能不变,中位数可能变小 |
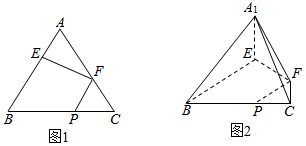 在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)
在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)