题目内容
1．已知O为△ABC内一点，且有$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$，记△ABC，△BCO，△ACO的面积分别为S1，S2，S3，则S1：S2：S3等于（ ）| A． | 3：2：1 | B． | 3：1：2 | C． | 6：1：2 | D． | 6：2：1 |
分析 如图所示，延长OB到点E，使得$\overrightarrow{OE}$=2$\overrightarrow{OB}$，分别以$\overrightarrow{OA}$，$\overrightarrow{OE}$为邻边作平行四边形OAFE．则$\overrightarrow{OA}$+2$\overrightarrow{OB}$=$\overrightarrow{OA}$+$\overrightarrow{OE}$=$\overrightarrow{OF}$，由于$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$，可得-$\overrightarrow{OF}$=3$\overrightarrow{OC}$．又$\overrightarrow{AF}$=2$\overrightarrow{OB}$，可得$\overrightarrow{DF}$=2$\overrightarrow{OD}$．于是$\overrightarrow{CO}$=$\overrightarrow{OD}$，得到S△ABC=2S△AOB．同理可得：S△ABC=3S△AOC，S△ABC=6S△BOC．即可得出．
解答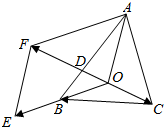 
解：如图所示，
延长OB到点E，使得$\overrightarrow{OE}$=2$\overrightarrow{OB}$，分别以$\overrightarrow{OA}$，$\overrightarrow{OE}$为邻边作平行四边形OAFE．
则$\overrightarrow{OA}$+2$\overrightarrow{OB}$=$\overrightarrow{OA}$+$\overrightarrow{OE}$=$\overrightarrow{OF}$，
∵$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$，∴-$\overrightarrow{OF}$=3$\overrightarrow{OC}$．
又$\overrightarrow{AF}$=2$\overrightarrow{OB}$，可得$\overrightarrow{DF}$=2$\overrightarrow{OD}$．
于是$\overrightarrow{CO}$=$\overrightarrow{OD}$，
∴S△ABC=2S△AOB．
同理可得：S△ABC=3S△AOC，S△ABC=6S△BOC．
∴ABC，△BOC，△ACO的面积比=6：1：2．
故选：C．
点评 本题考查了向量的平行四边形法则、向量共线定理、三角形的面积计算公式．
| A． | a＞b-1 | B． | a＞b+1 | C． | |a|＞|b| | D． | （$\frac{1}{2}$）a＞（$\frac{1}{2}$）b |