Question

正方体ABCD-A₁B₁C₁D₁中，P，Q分别是线段（不包括端点）CC₁，BD上的点，PQ∥ABC₁D₁，记CP=x，四面体PQA₁B₁的体积为y，则y关于x的函数大致图象是（　　）

• A、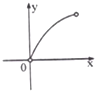
• B、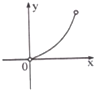
• C、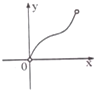
• D、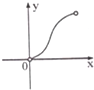

Answer 1

考点：函数的图象

专题：函数的性质及应用,空间向量及应用

分析：设正方体的棱长为1，过Q作QE⊥BC与E，得到面PQE∥面ABC₁D₁，得到CP=CE，建立空间坐标系，利用向量的数量积求出四面体的高，即Q到面A₁B₁P的距离，利用三棱锥的体积公式构造关于线段CP的长度为x的关系式，根据解析式选择函数图象．

解答： 解：设正方体的棱长为1，过Q作QE⊥BC与E，∴QE∥AB，
∵PQ∥ABC₁D₁，
∴面PQE∥面ABC₁D₁，
∴CP=CE，
以C为坐标原点，CC₁所在的直线为x轴，CB所在直线为Y轴，CD所在直线为Z轴，建立空间直角坐标系，
那么C（0，0，0），P（x，0，0），A₁（1，1，1），B₁（1，1，0），Q（0，x，1-x），
四面体PQA₁B₁的体积为y，△A₁B₁P面积为S，Q到面A₁B₁P的距离为d，则y=

1

3

Sd=

1

6

1+(1-x)2

d，设

n

为面A₁B₁P的法向量，由

n • A1B1 =0 n • B1P =0

，得

n

=（1，x-1，0），
∴d=

n • PQ

1+(x-1)2

=

2x-x2

x2-2x

=-

x2-2x

，
∴y=-

1

6

1+(1-x)2

x2-2x

=-

1

6

(x2-2x)=-

1

6

（x-1）²+

1

6

，x∈（0，1），由此y关于x的函数大致图象是A；
故选A．

点评：解决本题的关键是借助于空间坐标系，通过向量的数量积求出四面体的高，同时考查了空间想象能力及推理能力．