题目内容
已知⊙O:x2+y2=4的两条弦AB,CD互相垂直,且交于点M(1,
),则AB+CD的最大值为 .
| 2 |
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:由于直线AB、CD均过M点,故可以考虑设两个直线的方程为点斜式方程,但由于点斜式方程不能表示斜率不存在的情况,故要先讨论斜率不存在和斜率为0的情况,然后利用弦长公式,及基本不等式进行求解.
解答:
解:当AB的斜率为0或不存在时,可求得AB+CD=2(
+
)
当AB的斜率存在且不为0时,设直线AB的方程为y-
=k(x-1),
直线CD的方程为y-
=-
(x-1),
由弦长公式可得:AB2=4•
,CD2=
,
∴AB2+CD2=20
∴(AB+CD)2=AB2+CD2+2AB×CD≤2(AB2+CD2)=40
故AB+CD≤2
,即AB+CD的最大值为2
.
故答案为:2
.
| 2 |
| 3 |
当AB的斜率存在且不为0时,设直线AB的方程为y-
| 2 |
直线CD的方程为y-
| 2 |
| 1 |
| k |
由弦长公式可得:AB2=4•
3k2+2
| ||
| k2+1 |
2k2-2
| ||
| k2+1 |
∴AB2+CD2=20
∴(AB+CD)2=AB2+CD2+2AB×CD≤2(AB2+CD2)=40
故AB+CD≤2
| 10 |
| 10 |
故答案为:2
| 10 |
点评:本题考查直线与圆的位置关系,直线方程的应用,基本不等式的应用,点到直线的距离公式,考查转化思想与计算能力.

练习册系列答案
相关题目
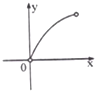
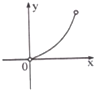
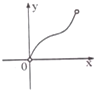
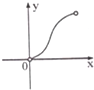
设f(x)是定义域为R的偶函数,且对任意实数x,恒有f(x+1)=-f(x),已知x∈(0,1)时,f(x)=log
(1-x),则函数f(x)在(1,2)上( )
| 1 |
| 2 |
| A、是增函数,且f(x)<0 |
| B、是增函数,且f(x)>0 |
| C、是减函数,且f(x)<0 |
| D、是减函数,且f(x)>0 |
已知从一点P引出三条射线PA、PB、PC,且两两成60°角,那么直线PC与平面PAB所成角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知方程
=k在(0,+∞)上有两个不同的解a,b(a<b),则下面结论正确的是( )
|cos(x-
| ||
| x |
| A、sina=acosb |
| B、sina=-acosb |
| C、cosa=bsinb |
| D、sinb=-bsina |
 如图,已知菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠ABE=60°,点H、G分别是线段EF、BC的中点.
如图,已知菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠BAD=∠CDA=90°,∠ABE=60°,点H、G分别是线段EF、BC的中点.