题目内容
12.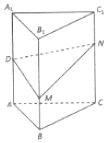 如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.
如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.①△DMN可能是直角三角形;②三棱锥A1-DMN的体积为定值;③平面DMN⊥平面BCC1B1;④平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$].
分析 ①,利用反证法思想说明△DMN不可能为直角三角形;
②,由△A1DM的面积不变,N到平面A1DM的距离不变,得到三棱锥A1-DMN的体积为定值;
③,由BM=C1N,得线段MN必过正方形BCC1B1的中心O,由DO⊥平面BCC1B1,可得平面DMN⊥平面BCC1B1;
④,平面DMN与平面ABC平行时所成角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大.
解答 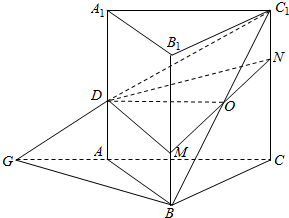 解:如图,
解:如图,
对于①,若△DMN为直角三角形,则必是以∠MDN为直角的直角三角形,但MN的最大值为BC1,而此时DM,DN的长大于BB1,∴△DMN不可能为直角三角形,故错误;
对于②,当M、N分别在BB1、CC1上运动时,△A1DM的面积不变,N到平面A1DM的距离不变,∴棱锥N-A1DM的体积不变,即三棱锥A1-DMN的体积为定值,故正确;
对于③,当M、N分别在BB1、CC1上运动时,若满足BM=C1N,则线段MN必过正方形BCC1B1的中心O,而DO⊥平面BCC1B1,∴平面DMN⊥平面BCC1B1,故正确;
对于④,当M、N分别为BB1,CC1中点时,平面DMN与平面ABC所成的角为0,当M与B重合,N与C1重合时,平面DMN与平面ABC所成的锐二面角最大,为∠C1BC,等于$\frac{π}{4}$.∴平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$],故正确,
∴正确的是②③④.
故答案为:②③④.
点评 本题考查了命题的真假判断与应用,考查了棱柱的结构特征,考查了空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
4.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( )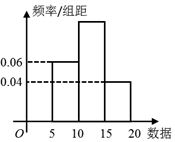

| A. | 12.5 11 | B. | 12.5 12 | C. | 12.5 13 | D. | 12.5 14 |
2.下列函数中是奇函数,且最小正周期是π的函数是( )
| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
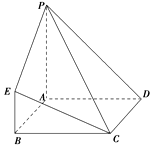 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )
已知函数y=2sin(ωx+φ)(0<ω<2π)的部分图象如图所示,点A($-\frac{π}{6}$,0),B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则$(\overrightarrow{AD}-\overrightarrow{EA})•(ω\overrightarrow{AC})$的值是( )