题目内容
在△ABC中,sinA+cosA=
,求tanA的值.
| ||
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式与sin2A+cos2A=1联立,求出sinA与cosA的值,将已知等式两边平方求出2sinAcosA的值,即为sin2A的值小于0,确定出A的范围,判断得到满足题意sinA与cosA的值,即可求出tanA的值.
解答:
解:联立得:
,
解得:
或
,
由sinA+cosA=
两边平方得:(sinA+cosA)2=1+2sinAcosA=
,即2sinAcosA=sin2A=-
,
∴180°<2A<360°,即90°<A<180°,
∴cosA<0,sinA>0,
∴sinA=
,cosA=
,
则tanA=
=-2-
.
|
解得:
|
|
由sinA+cosA=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴180°<2A<360°,即90°<A<180°,
∴cosA<0,sinA>0,
∴sinA=
| ||||
| 4 |
| ||||
| 4 |
则tanA=
| ||||||
|
| 3 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
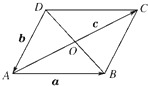 如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设
如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设