题目内容
已知两定点F1(- ,0),F2(
,0),F2( ,0),满足条件|PF2|-|PF1|=2的点P的轨迹是曲线E.
,0),满足条件|PF2|-|PF1|=2的点P的轨迹是曲线E.
(1)求曲线E的方程;
(2)设过点(0,-1)的直线与曲线E交于A,B两点.如果|AB|=6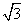 ,求直线AB的方程.
,求直线AB的方程.
 |
(1)解:由双曲线的定义可知,曲线E是以F1(- ,0),F2(
,0),F2( ,0)为焦点的双曲线的左支,且c=
,0)为焦点的双曲线的左支,且c= ,a=1,易知b=1,故曲线E的方程为x2-y2=1(x<0).
,a=1,易知b=1,故曲线E的方程为x2-y2=1(x<0).
(2)设A(x1,y1),B(x2,y2),由题意建立方程组
消去y,得(1-k2)x2+2kx-2=0,又已知直线与双曲线左支交于两点A,B,有
 解得-
解得- <k<-1.
<k<-1.
又∵|AB|= ·|x1-x2|=
·|x1-x2|= ·
·
= ·
· =2
=2 ,
,
依题意得2 =6
=6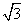 ,整理后得28k4-55k2+25=0,
,整理后得28k4-55k2+25=0,
∴k2= 或k2=
或k2= ,又-
,又- <k<-1,∴k=-
<k<-1,∴k=- ,故直线AB的方程为
,故直线AB的方程为 x+y+1=0.
x+y+1=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,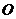 是坐标原点,两定点
是坐标原点,两定点 满足
满足 ,则点集
,则点集 所表示的区域的面积为( ).
所表示的区域的面积为( ). B.
B. C.
C. D.
D.
 与其关于点
与其关于点 对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为
对称的抛物线有两个不同的交点,若过这两个交点的直线的倾斜角为 ,则实数
,则实数 的值为______________.
的值为______________. ”是“
”是“ ”的()
”的() 的前n项和为
的前n项和为 ,若
,若 ,则公差
,则公差 ___________.
___________. 中,
中, ,则
,则 =( )
=( )