题目内容
14.已知命题p:方程$\frac{{x}^{2}}{2m-1}$+$\frac{{y}^{2}}{m-1}$=1表示的曲线是焦点在x轴的双曲线;命题q:关于m的不等式m2-(2a+1)m+a(a+1)≤0成立.(1)若a=$\frac{1}{2}$,且p∧q为真,求实数m的取值范围.
(2)若p是q的充分不必要条件,求实数a的取值范围.
分析 (1)由p∧q为真,可得p真且q真,P真:则设A={m|$\left\{{\begin{array}{l}{2m-1>0}\\{m-1<0}\end{array}}\right.$},q真:B={m|m2-(2a+1)m+a(a+1)≤0}={m|a≤m≤a+1},由$a=\frac{1}{2}$,可得B,即可得出A∩B.
(2)由(1)知设A={m|$\frac{1}{2}<m<1$},B={a≤m≤a+1},由p是q的充分不必要条件,可得A是B的真子集,即可得出.
解答 解:(1)∵p∧q为真,∴p真且q真 …(1分)
P真:则设A={m|$\left\{{\begin{array}{l}{2m-1>0}\\{m-1<0}\end{array}}\right.$}=$\{m|\frac{1}{2}<m<1\}$,…(2分)
q真:B={m|m2-(2a+1)m+a(a+1)≤0}={m|a≤m≤a+1}…(3分)
∵$a=\frac{1}{2}$,∴B=$\{m|\frac{1}{2}≤m≤\frac{3}{2}\}$…(4分)
∴A∩B=$\{m|\frac{1}{2}<m<1\}$
∴实数m的取值范围为:$\{m|\frac{1}{2}<m<1\}$…(6分)
(2)由(1)知设A={m|$\frac{1}{2}<m<1$},B={a≤m≤a+1}…(8分)
∵p是q的充分不必要条件,∴A是B的真子集
∴$\left\{{\begin{array}{l}{a≤\frac{1}{2}}\\{a+1≥1}\end{array}}\right.$…(10分)
解得$0≤a≤\frac{1}{2}$,…(11分)
∴实数a的取值范围为:$\{a|0≤a≤\frac{1}{2}\}$.…(12分)
点评 本题考查了简易逻辑的应用、不等式解法、集合的运算性质,考查了推理能力与计算能力,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | c>b>a | B. | b>c>a | C. | c>a>b | D. | a>b>c |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| 气温(°C) | 20 | 16 | 12 | 4 |
| 用电量(度) | 14 | 28 | 44 | 62 |
| A. | 70 | B. | 68 | C. | 64 | D. | 62 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
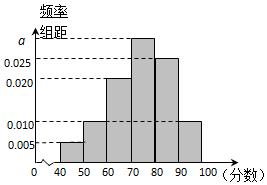 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.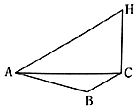 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,A,B,C三地位于同一水平面上,这种仪器在C地进行弹射实验,观测点A,B两地相距100米,∠BAC=60°,在A地听到弹射声音比B地晚$\frac{2}{17}$秒(已知声音传播速度为340米/秒),在A地测得该仪器至高点H处的仰角为30°,则这种仪器的垂直弹射高度HC=140$\sqrt{3}$米.