题目内容
1.已知命题p:函数y=ax是减函数,q:?x∈R,x2+x+a>0,若p∨q为真命题.p∧q为假命题,求实数a的取值范围.分析 由p∨q为真命题.p∧q为假命题知:命题p,q一真一假,进而得到实数a的取值范围.
解答 解:若命题p:函数y=ax是减函数为真命题,
则0<a<1,
若命题q:?x∈R,x2+x+a>0为真命题,
则a>$\frac{1}{4}$,
∵p∨q为真命题.p∧q为假命题,
∴命题p,q一真一假,
p真q假时,0<a≤$\frac{1}{4}$,
p假q真时,a≥1,
综上可得:0<a≤$\frac{1}{4}$,或a≥1.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数,函数恒成立问题,难度中档.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
11.正项等比数列{an}中,存在两项am、an使得$\sqrt{{a_m}•{a_n}}=2{a_1}$,且a6=a5+2a4,则$\frac{1}{m}+\frac{4}{n}$的最小值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{9}{4}$ |
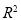 的值判断的拟合效果,
的值判断的拟合效果,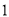 ;
;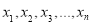 的方差为
的方差为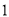 ,则
,则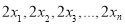 的方差为
的方差为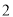 ;
;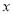 与
与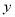 的随机变量
的随机变量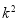 的观测值
的观测值 来说,
来说, 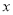 与
与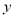 有关系”的把握程度越大.
有关系”的把握程度越大.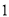 B.
B.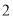 C.
C.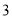 D.
D.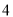
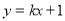 与圆
与圆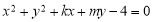 交于
交于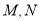 两点,且
两点,且 关于直线
关于直线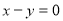 对称,动点P
对称,动点P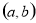 在不等式组
在不等式组 表示的平面区域内部及边界上运动,则
表示的平面区域内部及边界上运动,则 的取值范围是( )
的取值范围是( )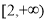 B.
B.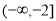
 D.
D.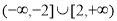
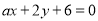 与l2:
与l2: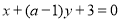 平行,那么a等于( )
平行,那么a等于( )